Chapter 8 Mean Value Theorems-II

Formulas for the expansion

Taylor’s theorem in finite form with Lagrange’s form of remainder

\[\begin{equation*} \begin{split} f(a+h) &= f(a) + hf'(a) + \frac{h^2}{2!}f''(a) + \ldots + \frac{h^{n-1}}{(n-1)!}f^{n-1}(a) + \\ & \frac{h^n}{n!} f^n(a+\theta h) \end{split} \end{equation*}\]

where $0 < \theta < 1$

The term $\frac{h^n}{n!} f^n(a+\theta h)$ is the remainder $R_n$.

Taylor’s theorem in finite form with Cauchy’s form of remainder

\[\begin{equation*} \begin{split} f(a+h) &= f(a) + hf'(a) + \frac{h^2}{2!}f''(a) + \ldots + \frac{h^{n-1}}{(n-1)!}f^{n-1}(a) + \\ & \frac{h^n}{(n-1)!} (1-\theta)^{n-1} f^n(a+\theta h) \end{split} \end{equation*}\]

where $0 < \theta < 1$

The term $\frac{h^n}{(n-1)!} (1-\theta)^{n-1} f^n(a+\theta h)$ is the remainder $R_n$.

Maclaurin’s series in finite form with Lagrange’s form of remainder

\[\begin{equation*} \begin{split} f(x) &= f(0) + \frac{x}{1!}f'(0) + \frac{x^2}{2!}f''(0) + \ldots + \frac{x^{n-1}}{(n-1)!}f^{n-1}(0) + \\ & \frac{x^n}{n!} f^n(\theta x) \end{split} \end{equation*}\]

where $0 < \theta < 1$

The term $\frac{x^n}{n!} f^n(\theta x)$ is the remainder $R_n$.

Maclaurin’s series in finite form with Cauchy’s form of remainder

\[\begin{equation*} \begin{split} f(x) &= f(0) + \frac{x}{1!}f'(0) + \frac{x^2}{2!}f''(0) + \ldots + \frac{x^{n-1}}{(n-1)!}f^{n-1}(0) + \\ & \frac{x^n}{(n-1)!} (1- \theta)^{n-1} f^n(\theta x) \end{split} \end{equation*}\]

where $0 < \theta < 1$

The term $\frac{x^n}{(n-1)!} (1- \theta)^{n-1} f^n(\theta x)$ is the remainder $R_n$.

Taylor’s series in infinite series

\[\begin{equation*} \begin{split} f(x+h) &= f(x) + h f'(x) + \frac{h^2}{2!} f''(x) + \frac{h^3}{3!}f'''(x) + \ldots \end{split} \end{equation*}\]

Maclaurin’s series in infinite series

Maclaurin Series Expansion is a Taylor Series Expansion centered at 0.

8.0.1 Few expansions to remember

\[\begin{equation*} \begin{split} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}+ \ldots\\ \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots\\ \cos x &= 1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots\\ \tan x &= x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\\ \log (1+x) &= x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5}- \ldots \\ \end{split} \end{equation*}\]

8.0.2 Question 1

For each of the following functions prove that $R_n \rightarrow 0$ as $n \rightarrow \infty$ and write down the power series expansion of each.

$\boldsymbol{\cos x}$

Let $f(x) = \cos x$.

We know the Maclaurin’s series with Lagrange’s form of remainder,

\[\begin{equation*} \begin{split} f(x) &= f(0) + \frac{x}{1!}f'(0) + \frac{x^2}{2!}f''(0) + \ldots + \frac{x^{n-1}}{(n-1)!}f^{n-1}(0) + \\ \frac{x^n}{n!} f^n(\theta x) \end{split} \end{equation*}\]

Then,

\[\begin{equation*} \begin{split} f^n (x) &= \cos (x + n\pi/2)\\ f^n (\theta x) &= \cos (\theta x + n\pi/2)\\ R_n &= \frac{x^n}{n!}f^n (\theta x)\\ &= \frac{x^n}{n!} \cos (\theta x + n\pi/2) \end{split} \end{equation*}\]

As $n \rightarrow \infty$, $R_n \rightarrow 0$ for all values of $x$. Thus conditions for Maclaurin’s expansion for infinite series is valid.

Also,

\[\begin{equation*} \begin{split} f(0) &= 1 \\ f'(0) &= \cos (0 + \pi/2) = 0\\ f''(0) &= \cos (0 + 2\pi/2) = -1 \\ f'''(0) &= \cos (0 + 3\pi/2) = 0 \\ f^4 (0) &= \cos (0 + 4\pi/2) = 1 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots \\ &= 1 + 0 -\frac{x^2}{2!} + 0 + \frac{x^4}{4!} + 0 - \frac{x^6}{6!} + \ldots \\ \cos x &= 1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \end{split} \end{equation*}\]

$\boldsymbol{\sin^2 x}$

Let $f(x) = \sin^2 x = \frac{1- \cos 2x}{2}$.

\[\begin{equation*} \begin{split} f^n (x) &= 0 - \frac{1}{2}\times 2^n \cos (2x+ n \pi/2) = -2^{n-1} \cos (2x+ n \pi/2)\\ f^n (\theta x) &= -2^{n-1} \cos (2 \theta x+ n \pi/2)\\ R_n &= \frac{x^n}{n!}f^n (\theta x)\\ &= - \frac{x^n}{n!} 2^{n-1} \cos (2 \theta x+ n \pi/2) \end{split} \end{equation*}\]

As $n \rightarrow \infty$, $R_n \rightarrow 0$ for all values of $x$. Thus conditions for Maclaurin’s expansion for infinite series is valid.

Also,

\[\begin{equation*} \begin{split} f(0) &= 0 \\ f'(0) &= -2^0 \cos (0 + \pi/2) = 0 \\ f''(0) &= -2^{2-1} \cos ( 0 + 2\pi/2) = 2\\ f'''(0) &= -2^2 \cos ( 0 + 3\pi/2) = 0\\ f^4 (0) &= -2^3 \cos ( 0 + 4\pi/2) = -2^3\\ f^5 (0) &= -2^4 \cos ( 0 + 5\pi/2) = 0\\ f^6 (0) &= -2^5 \cos ( 0 + 6\pi/2) = 2^5 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots \\ \sin^2 x &= 0 + 0 + \frac{2x^2}{2!} + 0 - \frac{2^3x^4}{4!} + 0 + \frac{2^5 x^6}{6!} - \ldots \\ &= \frac{1}{2} \left \{\frac{(2x)^2}{2!} + 0 - \frac{(2x)^4}{4!} + 0 + \frac{(2x)^6}{6!} - \ldots \right\}\\ &= \frac{1}{2} \left \{\frac{(2x)^2}{2!} - \frac{(2x)^4}{4!} + \frac{(2x)^6}{6!} - \ldots \right\} \end{split} \end{equation*}\]

\[\begin{equation} \begin{split} \sin^2 x &= \frac{1}{2} \left \{\frac{(2x)^2}{2!} - \frac{(2x)^4}{4!} + \frac{(2x)^6}{6!} - \ldots \right\} \end{split} \tag{8.1} \end{equation}\]

$\boldsymbol{\cos^2 x}$

We know,

\[\begin{equation*} \begin{split} \cos^2 x &= 1 - \sin^2 x\\ \end{split} \end{equation*}\]

From the expansion of $\sin^2 x$ in (8.1), we have,

\[\begin{equation*} \begin{split} \cos^2 x &= 1- \frac{1}{2} \left \{\frac{(2x)^2}{2!} - \frac{(2x)^4}{4!} + \frac{(2x)^6}{6!} - \ldots \right\} \end{split} \end{equation*}\]

$\boldsymbol{\log(1-x)}$

Let $y = f(x) = \log (1-x)$.

General equation for higher derivatives of the given function is,

\[\begin{equation*} \begin{split} f^n (x) &=\frac{(n-1)! (-1)^{2n-1}}{(1-x)^n} \end{split} \end{equation*}\]

So,

\[\begin{equation*} \begin{split} f(0) &= 0\\ f'(0) &= -1\\ f''(0) &= -1\\ f'''(0) &= -2!\\ f^4 (0) &= -3! \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots \\ \log(1-x) &= 0 - \frac{x}{1!} - \frac{x^2}{2!} - \frac{2! x^3}{3!} - \frac{3! x^4}{4!}- \ldots\\ \log(1-x) &= - x - \frac{x^2}{2} - \frac{x^3}{3} - \frac{x^4}{4}- \ldots\\ \end{split} \end{equation*}\]

$\boldsymbol{\frac{1}{(1+x)}}$

Let $y= f(x) = \frac{1}{1+x}$.

\[\begin{equation*} \begin{split} f'(x) &= (-1) (1+x)^{-2}\\ f''(x) &= (-1)^2 2! (1+x)^{-3}\\ f'''(x) &= (-1)^3 3! (1+x)^{-4} \end{split} \end{equation*}\]

So general form for higher derivatives is,

\[\begin{equation*} \begin{split} f^n (x) &= \frac{(-1)^n n!}{(1+x)^{n+1}} \end{split} \end{equation*}\]

Calculating higher derivatives for $x=0$,

\[\begin{equation*} \begin{split} f(0) &= 1\\ f'(0) &= -1\\ f''(0) &= 2! \\ f'''(0) &= -3! \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ \frac{1}{1+x} &= 1 - x + \frac{2! x^2}{2!} - \frac{3! x^3}{3!} + \ldots \\ &= 1- x + x^2 -x^3 +x^4 - \ldots \end{split} \end{equation*}\]

8.0.3 Question 2

Expand in ascending powers of x

$\boldsymbol{(1+x)^m}$

Let $y=f(x) = (1+x)^m$.

Differentiating successively,

\[\begin{equation*} \begin{split} f'(x) &= m(1+x)^{m-1}\\ f''(x) &= m(m-1)(1+x)^{m-2}\\ f'''(x) &= m(m-1)(m-2)(1+x)^{m-3}\\ f^n (x) &= \frac{m!}{(m-3)!}(1+x)^{m-n} \end{split} \end{equation*}\]

Calculating higher derivatives at $x=0$,

\[\begin{equation*} \begin{split} f(0) &= 1 \\ f'(0) &= m \\ f''(0) &= m(m-1)\\ f'''(0) &= m(m-1)(m-2) \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

$\boldsymbol{\tan \text{h}x}$

Let $\tan \text{h}x = \frac{\sin \text{h}x}{\cos \text{h}x}= \frac{f(x)}{g(x)}$. We have to find individual expansion of $f(x)=\sin \text{h}x$ and $g(x) = \cos \text{h}x$ and divide $f(x)$ by $g(x)$ to find the required expansion.

We have,

\[\begin{equation*} \begin{split} f(x) &= \sin \text{h}x & \Longrightarrow f(0) = 0\\ f'(x) &= \cos \text{h}x & \Longrightarrow f'(0) = 1\\ f''(x) &= \sin \text{h}x & \Longrightarrow f''(0) = 0\\ f'''(x) &= \cos \text{h}x & \Longrightarrow f'''(0) = 1\\ f^4 (x) &= \sin \text{h}x & \Longrightarrow f^4 (0) = 0 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

Similarly,

\[\begin{equation*} \begin{split} g(x) &= \cos \text{h}x & \Longrightarrow g(0) = 1\\ g'(x) &= \sin \text{h}x & \Longrightarrow g'(0) = 0\\ g''(x) &= \cos \text{h}x & \Longrightarrow g''(0) = 1\\ g'''(x) &= \sin \text{h}x & \Longrightarrow g'''(0) = 0\\ g^4 (x) &= \cos \text{h}x & \Longrightarrow g^4 (0) = 1\\ \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} g(x) &= g(0) + xg'(0) + \frac{x^2}{2!}g''(0) + \frac{x^3}{3!}g'''(0) + \\ & \frac{x^4}{4!}g^4 (0) + \frac{x^5}{5!}g^5 (0) + \frac{x^6}{6!}g^6 (0) + \ldots\\ \cos \text{h}x &= 1 + \frac{x^2}{2!} + \frac{x^4}{4!} + \frac{x^6}{6!} + \ldots \end{split} \end{equation*}\]

Now,

\[\begin{equation*} \begin{split} \tan \text{h}x &= \frac{\sin \text{h}x}{\cos \text{h}x} = \frac{f(x)}{g(x)}\\ &= \frac{x + \frac{x^3}{3!} + \frac{x^5}{5!}+ \ldots }{1 + \frac{x^2}{2!} + \frac{x^4}{4!} + \frac{x^6}{6!} + \ldots}\\ &= x- \frac{2}{3!}x^3 + \frac{16}{5!}x^5 - \ldots \end{split} \end{equation*}\]

How this division is carried out is shown here,

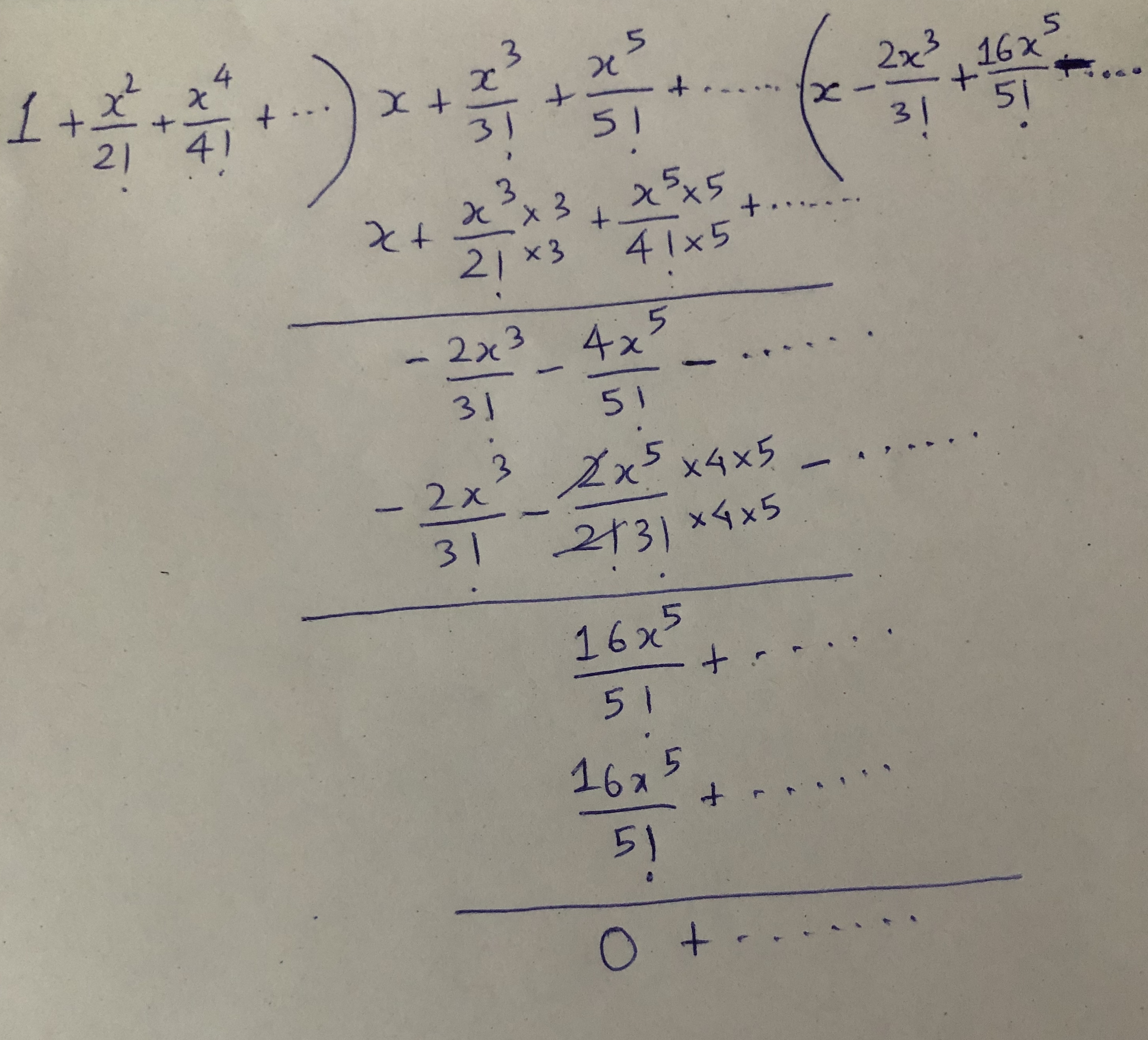
Figure 8.1: Division of two expansions

For inspiration of such division, see this video.

8.0.4 Question 3

Expand $\tan x$ in the ascending integral powers of $x$ using Maclaurin’s series and hence get the expansion of $\sec^2 x$.

We know $\tan x = \frac{\sin x}{\cos x}$. We also know the expansions as follow:

\[\begin{equation*} \begin{split} \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots \\ \cos x &= 1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \end{split} \end{equation*}\]

Thus,

\[\begin{equation*} \begin{split} \tan x &= \frac{x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots}{1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots}\\ \end{split} \end{equation*}\]

By division as shown in figure below, we have

\[\begin{equation*} \begin{split} \tan x &= x + \frac{1}{3}x^3 + \frac{2}{15}x^5+ \frac{17}{315}x^7 + \ldots \end{split} \end{equation*}\]

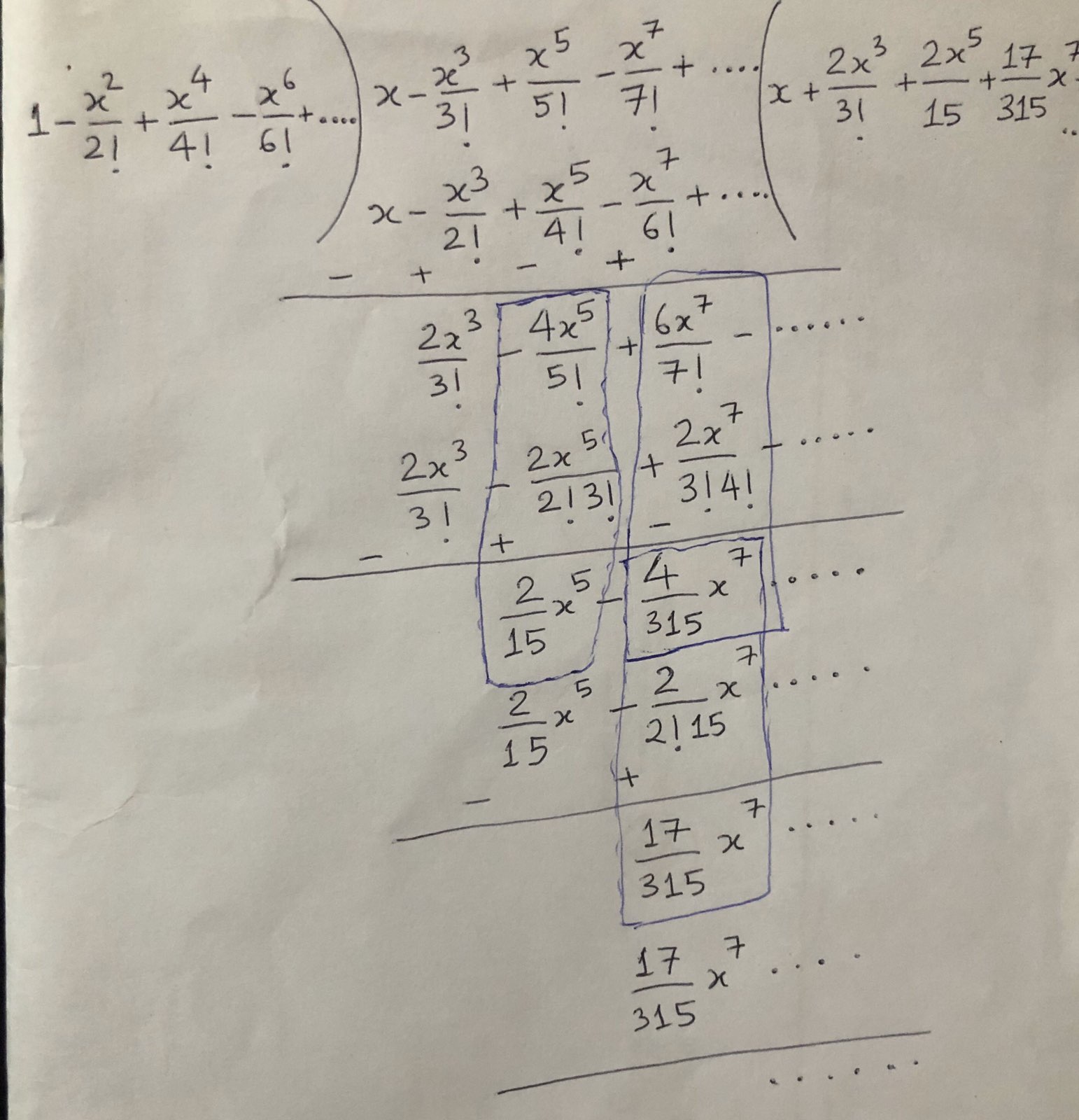
$Division of $\sin x$ by $\cos x$$

Figure 8.2: Division of $\sin x$ by $\cos x$

Differentiating both sides w.r.t $x$,

\[\begin{equation*} \begin{split} \sec^2 x &= 1 + \frac{3x^2}{3} + \frac{2\times 5 x^4}{15} + \frac{17 \times 7 x^6 }{315} + \ldots \\ &= 1 + x^2 + \frac{2}{3}x^4 + \frac{17}{45}x^6 + \ldots \end{split} \end{equation*}\]

Obtain the series expansion of $e^{\sin x}$ by Maclaurin’s theorem as far as the term $x^4$.

Let $f(x) = e^{\sin x}$.

\[\begin{equation*} \begin{split} f'(x) &= e^{\sin x} \cos x = f(x) \cos x\\ f''(x) &= f'(x) \cos x - f(x) \sin x \\ f'''(x) &= f''(x) \cos x - f'(x)\sin x - (f(x)\cos x + f'(x) \sin x)\\ &= f''(x) \cos x - 2f'(x) \sin x - f'(x)\\ f^4 (x) &= f'''(x) \cos x - f''(x) \sin x - 2(f'(x)\cos x + f''(x)\sin x) - f''(x)\\ &= f'''(x) \cos x - 3f''(x) \sin x - 2f'(x) \cos x - f''(x) \end{split} \end{equation*}\]

Calculating higher order derivatives at $x=0$,

\[\begin{equation*} \begin{split} f(0) &= 1\\ f'(0) &= 1 \times 1 = 1\\ f''(0) &= 1 - 0 = 1\\ f'''(0) &= 1-0-1 = 0 \\ f^4 (0) &= 0 - 0 -2 -1 = -3\\ f^5 (0) &= f^4 (0) \cos 0 - 3 f''(0) \cos 0 - 2f''(0) \cos 0- f'''(0)\\ &= - 3 -3-2-0 =-8 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ e^{\sin x} &= 1 + x + \frac{x^2}{2!}\times 1 + 0 + \frac{x^4}{4!}\times (-3) + \frac{x^5}{5!} \times (-8) \ldots\\ &= 1 + x + \frac{x^2}{2} - \frac{x^4}{8} - \frac{x^5}{15} \ldots\\ \end{split} \end{equation*}\]

I have answered this question in Math StackExchange too.

Find the power series expansion of $e^x \sin x$ by Maclaurin’s theorem upto $x^4$.

Let $y= f(x) = e^x \sin x$.

\[\begin{equation*} \begin{split} f'(x) &= e^x \cos x + e^x \sin x\\ f''(x) &= e^x \cos x - e^x \sin x + e^x \cos x + e^x \sin x \\ &= 2 e^x \cos x \\ f'''(x) &= 2(e^x \cos x - e^x \sin x)\\ f^4 (x) &= 2(e^x \cos x - e^x \sin x - e^x \cos x - e^x \sin x)\\ &= -4 e^x \sin x\\ f^5 (x) &= -4(e^x \cos x + e^x \sin x) \end{split} \end{equation*}\]

Other way of finding successive derivatives is the formula in the chapter on higher derivatives,

\[\begin{equation*} \begin{split} f(x) &= e^x \sin x \\ f^n (x) &= (1^2 + 1^2)^{n/2} e^x \sin (x + n \tan^{-1} 1)\\ &= 2^{n/2} e^x \sin( x + n\pi/4)\\ f^n(0) &= 2^{n/2} \sin \left(\frac{n\pi}{4}\right) \end{split} \end{equation*}\]

Calculating higher derivatives at $x=0$,

\[\begin{equation*} \begin{split} f(0) &= 0\\ f'(0) &= 1\\ f''(0) &= 2\\ f'''(0) &= 2\\ f^4 (0) &= 0 \\ f^5 (0) &= -4 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ e^x \sin x &= 0 + x + \frac{x^2}{2!}\times 2 + \frac{x^3}{3!} \times 2 + 0 + \frac{x^5}{5!} \times (-4) \ldots \\ e^x \sin x &= x + x^2 + \frac{x^3}{3} - \frac{x^5}{30} \ldots \\ \end{split} \end{equation*}\]

Expand $\log (1+\sin x)$ with the help of Maclaurin’s theorem as far as the term involving $x^4$.

Let $f(x) = \log (1+\sin x)$.

\[\begin{equation*} \begin{split} f'(x) &= \frac{\cos x}{1+ \sin x}\\ f''(x) &= \frac{-\sin x(1+ \sin x) - \cos^2 x}{(1+ \sin x)^2}\\ &= \frac{-\sin x - \sin^2 x - \cos^2 x}{(1+\sin x)^2}\\ &= -\frac{1}{1+ \sin x}\\ f'''(x) &= \frac{\cos x}{(1 + \sin x)^2}\\ f^4 (x) &= \frac{- \sin x (1+ \sin x)^2 - \cos x(2(1+\sin x)\cos x)}{(1+\sin x)^4}\\ &= \frac{(1+\sin x)(-\sin x - \sin^2 x - 2\cos^2 x)}{(1+\sin x)^4}\\ &= -\frac{1 + \sin x + \cos^2 x}{(1 + \sin x)^3} \end{split} \end{equation*}\]

Calculating higher derivatives at $x=0$,

\[\begin{equation*} \begin{split} f(0) &= 0\\ f'(0) &= 1\\ f''(0) &= -1\\ f'''(0) &= 1\\ f^4 (0) &= -2 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ \log (1+\sin x) &= 0 + x + \frac{x^2}{2!} \times (-1) + \frac{x^3}{3!} \times (1) + \frac{x^4}{4!} \times (-2) + \ldots\\ \log (1+\sin x) &= x -\frac{x^2}{2} + \frac{x^3}{6} - \frac{x^4}{12} + \ldots \end{split} \end{equation*}\]

Instead of going through cumbersome successive derivatives, we can approach the problem in other way too,

\[\begin{equation*} \begin{split} \frac{\mathrm{d}}{\mathrm{dx}}\log (1+ \sin x) &= \frac{\cos x}{1 + \sin x}\\ &= \frac{1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots}{1 + x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots} \end{split} \end{equation*}\]

Integrating both sides after the result of division gives the desired result.

Apply Maclaurin’s series to find the expansion of $\frac{e^x}{1 + e^x}$ as far as the term in $x^3$ and hence the expansion of $\log (1+e^x)$.

The expansion of $e^x$ is,

\[\begin{equation*} \begin{split} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}+ \ldots \end{split} \end{equation*}\]

So,

\[\begin{equation*} \begin{split} 1 + e^x &= 1 + 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots\\ &= 2 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots \end{split} \end{equation*}\]

Thus,

\[\begin{equation*} \begin{split} \frac{e^x}{1 + e^x} &= \frac{1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots}{2 + x + \frac{x^2}{2!} + \frac{x^3}{3!}+ \ldots}\\ &= \frac{1}{2} + \frac{x}{4} - \frac{x^3}{48} + \frac{x^4}{96} \ldots \end{split} \end{equation*}\]

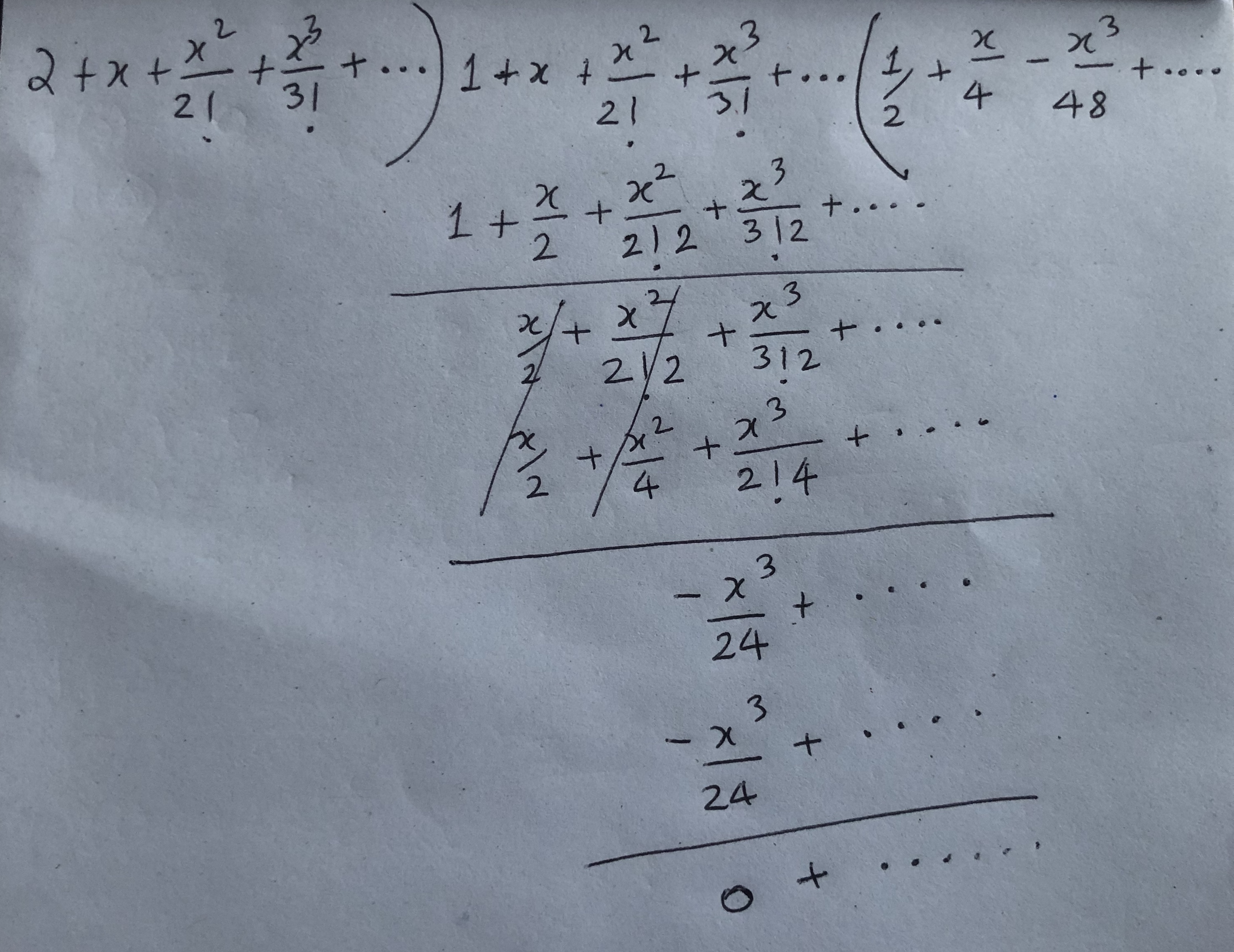
Figure 8.3: Figure showing divisions of $e^x$ by $1 + e^x$ expansion

For second part, let $f(x) = \log (1+e^x)$.

\[\begin{equation*} \begin{split} f(x) &= \log (1+e^x)\\ f(0) &= \log 2 \\ f'(x) &= \frac{e^x}{1+e^x} = \frac{1}{2} + \frac{x}{4} - \frac{x^3}{48} + \frac{x^4}{96} \ldots \\ f'(0) &= \frac{1}{2}\\ f''(x) &= \frac{1}{4} - \frac{3x^2}{48} + \frac{4x^3}{96} \ldots\\ f''(0) &= \frac{1}{4}\\ f'''(x) &= -\frac{6x}{48} + \frac{12x^2}{96} \ldots\\ f'''(0) &= 0\\ f^4 (x) &= -\frac{6}{48} + \frac{24x}{96} \ldots\\ f^4 (0) &= -\frac{6}{48} \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ \log(1+e^x) &= \log 2 + \frac{1}{2}x + \frac{x^2}{2!}\times \frac{1}{4} + 0 + \frac{x^4}{4!}\times \left(-\frac{6}{48}\right) + \ldots\\ &= \log 2 + \frac{x}{2} + \frac{x^2}{8} - \frac{x^4}{192} + \ldots \end{split} \end{equation*}\]

8.0.5 Question 4

Assuming the validity of expansion, prove the following series using Maclaurin’s theorem.

$\sec x = 1 + \frac{1}{2}x^2 + \frac{5}{24}x^4 + \ldots$

We know,

\[\begin{equation*} \begin{split} \cos x &= 1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots \end{split} \end{equation*}\]

Let,

\[\begin{equation} \begin{split} \sec x &= a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + \ldots \\ \end{split} \tag{8.2} \end{equation}\]

\[\begin{equation*} \begin{split} 1 &= (a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + \ldots) \cos x \\ 1 &= (a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + \ldots)(1 -\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots)\\ \end{split} \end{equation*}\]

Equating the constant term and the coefficients of $x, x^2, x^3, x^4$, we have,

\[\begin{equation*} \begin{split} a_0 &= 1 \\ a_1 &= 0\\ -\frac{a_0}{2!} + a_2 &= 0, \; a_2 = \frac{1}{2} \\ -\frac{a_1}{2!} + a_3 &= 0, \; a_3 = 0 \\ \frac{a_0}{4!} - \frac{a_2}{2!} + a_4 &= 0, \; a_4 = \frac{5}{24} \end{split} \end{equation*}\]

Replacing values of $a_0, a_1, a_2, a_3, a_4$ in (8.2), we have,

\[\begin{equation*} \begin{split} \sec x &= 1 + 0 + \frac{1}{2}x^2 + 0 + \frac{5}{24}x^4 + \ldots\\ &= 1 + \frac{1}{2}x^2 + \frac{5}{24}x^4 + \ldots \end{split} \end{equation*}\]

$\log (1 + \tan x) = x - \frac{x^2}{2!} + \frac{4}{3!}x^3 - \ldots$

Approaching this problem via successive derivatives is cumbersome. So we use algebraic method for expansion utilising what we know already.

What we know,

\[\begin{equation*} \begin{split} \tan x &= x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\\ \log (1+x) &= x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5}- \frac{x^6}{6} + \frac{x^7}{7} - \ldots \\ \end{split} \end{equation*}\]

So,

Lets find values of numerators in the fractions,

\[\begin{equation*} \begin{split} (\tan x)^2 &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right)^2 \\ &= x^2 + 2x\left(\frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right) + \left(\frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots \right)^2 \\ &= x^2 + \frac{2x^4}{3} + \frac{4x^6}{15} + \ldots + \frac{x^6}{9} + \ldots\\ &= x^2 + \frac{2x^4}{3} + \frac{17x^6}{45} + \ldots\\ (\tan x)^3 &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots \right)^3 \\ &= x^3 + 3x^2 \left(\frac{x^3}{3} + \frac{2x^5}{15} + \ldots\right) + 3x\left(\frac{x^3}{3} + \frac{2x^5}{15} + \ldots\right)^2 + \\ & \left(\frac{x^3}{3} + \frac{2x^5}{15} + \ldots\right)^3\\ &= x^3 + \frac{3x^5}{3} + \frac{6x^7}{15}+ \ldots + \frac{3x^7}{9} + \frac{12x^9}{45} + \ldots + \frac{x^9}{27} + \ldots \\ &= x^3 + \frac{3x^5}{3} + \frac{11x^7}{15}+ \ldots \\ (\tan x)^4 &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right)^4 \\ &= x^4 + 4x^3\left(\frac{x^3}{3} + \frac{2x^5}{15} + \ldots\right) + \ldots\\ &= x^4 + \frac{4x^6}{3} + \ldots\\ (\tan x)^5 &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right)^5 \\ &= x^5 + 5x^4\left(\frac{x^3}{3} + \frac{2x^5}{15} + \ldots\right) + \ldots\\ &= x^5 + \frac{5x^7}{3} + \ldots \\ (\tan x)^6 &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right)^6\\ &= x^6 + \ldots \\ (\tan x)^7 &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right)^7\\ &= x^7 + \ldots \end{split} \end{equation*}\]

Lets put these values in equation (8.3),

\[\begin{equation*} \begin{split} \log (1+\tan x) &= \tan x - \frac{(\tan x)^2}{2} + \frac{(\tan x)^3}{3} - \frac{(\tan x)^4}{4} + \frac{(\tan x)^5}{5}- \\ & \frac{(\tan x)^6}{6} + \frac{(\tan x)^7}{7}- \ldots \\ &= \left(x + \frac{x^3}{3} + \frac{2x^5}{15} + \frac{17}{315}x^7 + \ldots\right) - \frac{1}{2}\left(x^2 + \frac{2x^4}{3} + \frac{17x^6}{45} + \ldots\right) + \\ & \frac{1}{3}\left(x^3 + \frac{3x^5}{3} + \frac{11x^7}{15}+ \ldots\right) - \frac{1}{4}\left(x^4 + \frac{4x^6}{3} + \ldots\right) + \\ & \frac{1}{5}\left(x^5+ \frac{5x^7}{3} + \ldots\right) - \\ & \frac{1}{6}(x^6 + \ldots) + \frac{1}{7}(x^7 + \ldots) \end{split} \end{equation*}\]

Now collecting coefficients of $x, x^2, x^3, x^4, x^5, x^6, x^7$, we have,

$x$	$x^2$	$x^3$	$x^4$	$x^5$
$1$	$-\frac{1}{2}$	$\frac{1}{3} + \frac{1}{3} = \frac{2}{3}$	$-\frac{1}{3}-\frac{1}{4} =-\frac{7}{12}$	$\frac{2}{15} + \frac{1}{3} + \frac{1}{5}=\frac{2}{3}$

$x^6$	$x^7$
$-\frac{17}{90} - \frac{1}{3} - \frac{1}{6}= -\frac{31}{45}$	$\frac{17}{315}+ \frac{11}{45} + \frac{1}{3}+\frac{1}{7} =\frac{244}{315}$

So the expansion is,

\[\begin{equation*} \begin{split} \log (1+\tan x) &= x -\frac{1}{2}x^2 + \frac{2}{3}x^3 - \frac{7}{12}x^4 + \frac{2}{3}x^5 -\frac{31}{45}x^6 + \frac{244}{315}x^7 - \ldots \end{split} \end{equation*}\]

For a much easier approach, derivative of the function $\log (1+\tan x)$ is given by

\[\begin{align} \frac{\mathrm d}{\mathrm dx}\ln(1+\tan(x))&=\frac{\sec^2(x)}{1+\tan(x)}\\ &=\frac{1+\tan^2(x)}{1+\tan(x)}\\ &=\frac{1+\left(x+\frac13x^3+\frac2{15}x^5\right)^2}{1+x+\frac13x^3+\frac2{15}x^5}+\mathcal O(x^7)\\ &=\frac{1+x^2+\frac23x^4+\frac{17}{45}x^6}{1+x+\frac13x^3+\frac2{15}x^5}+\mathcal O(x^7)\\ &=1-x+2x^2-\frac73x^3+\frac{10}3x^4-\frac{62}{15}x^5+\frac{244}{45}x^6+\mathcal O(x^7) \end{align}\]

Integrating both sides,

$e^x \sec x = 1 + x + x^2 + \frac{2}{3}x^3 + \ldots$

\[\begin{equation*} \begin{split} e^x \sec x &= (1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}+ \ldots)\\ & (1 + \frac{1}{2}x^2 + \frac{5}{24}x^4 + \ldots)\\ &= 1 + x + \left(\frac{1}{2}+\frac{1}{2!}\right)x^2 + \\ & \left(\frac{1}{2}+\frac{1}{3!}\right)x^3 + \left(\frac{5}{24}+\frac{1}{2!2} + \frac{1}{4!}\right)x^4 + \ldots\\ &= 1 + x + x^2 + \frac{4}{6}x^3 + \frac{11}{24}x^4 + \ldots \\ &= 1 + x + x^2 + \frac{2}{3}x^3 + \frac{11}{24}x^4 + \ldots \\ \end{split} \end{equation*}\]

This video on YouTube is good to learn the concept of multiplication of two expansions.

$e^{ax} \cos bx = 1 + ax + (a^2-b^2)\frac{x^2}{2!} + a(a^2 - 3b^2)\frac{x^3}{3!} + \ldots$

\[\begin{equation*} \begin{split} y &= e^{ax} \cos bx \\ y_1 &= a e^{ax} \cos bx - b e^{ax} \sin bx \\ &= ay - b e^{ax} \sin bx \\ y_2 &= ay_1 - b(b e^{ax} \cos bx + a e^{ax} \sin bx) \\ &= ay_1 - b^2 y - ab e^{ax} \sin bx \\ y_3 &= ay_2 -b^2y_1 -ab(b e^{ax} \cos bx + a e^{ax} \sin bx)\\ &= ay_2 -b^2y_1 -ab^2y -a^2b e^{ax} \sin bx \end{split} \end{equation*}\]

\[\begin{equation*} \begin{split} (y)_0 &= 1\\ (y_1)_0 &= a\\ (y_2)_0 &= a^2 -b^2 \\ (y_3)_0 &= a(a^2-b^2) - ab^2 -ab^2 - 0\\ &= a(a^2 -3b^2) \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ e^{ax} \cos bx &= 1 + ax + (a^2 -b^2)\frac{x^2}{2!} + a(a^2 - 3b^2)\frac{x^3}{3!}+ \ldots \end{split} \end{equation*}\]

$\log(1 + x + x^2) = x + \frac{x^2}{2} - \frac{2}{3}x^3 + \frac{x^4}{4} + \ldots$

We know the expansion for $\log (1+x)$ is,

\[\begin{equation*} \begin{split} \log (1+x) &= x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5}- \ldots \\ \end{split} \end{equation*}\]

So,

\[\begin{equation*} \begin{split} \log (1+x+x^2) &= \log \{1+(x+x^2)\} \\ &= (x + x^2) - \frac{(x + x^2)^2}{2} + \frac{(x + x^2)^3}{3} - \frac{(x + x^2)^4}{4} + \frac{(x + x^2)^5}{5}- \ldots \end{split} \end{equation*}\]

Lets expand the expressions in the numerator using binomial expansion,

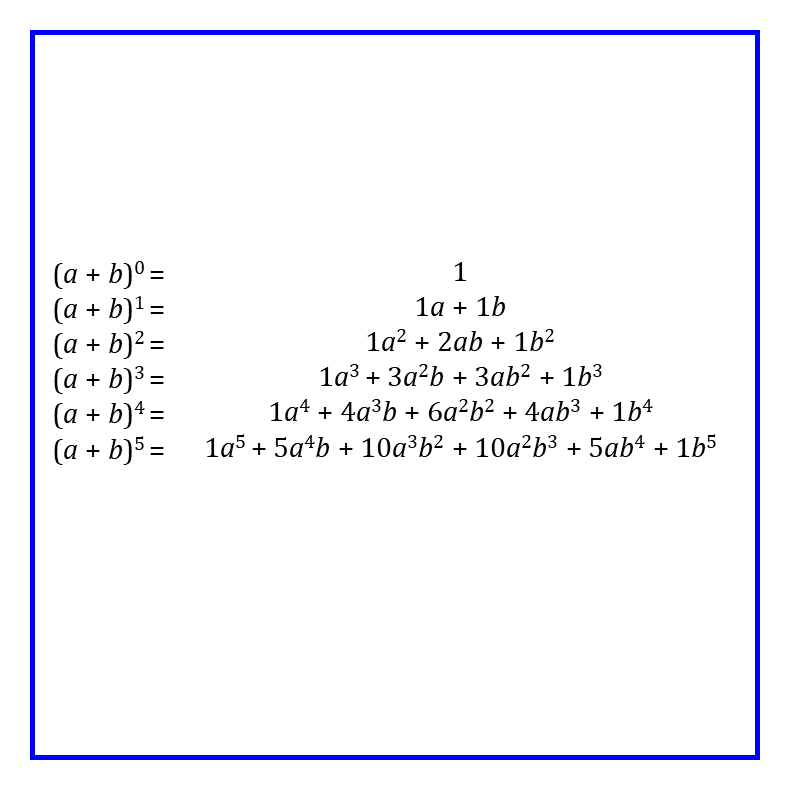
Figure 8.4: Binomial expansion

\[\begin{equation*} \begin{split} \log (1+x+x^2) &= (x + x^2) - \frac{(x + x^2)^2}{2} + \frac{(x + x^2)^3}{3} - \frac{(x + x^2)^4}{4} + \frac{(x + x^2)^5}{5}- \ldots \\ &= x + x^2 - \frac{x^2 + 2x^3 + x^4}{2} + \frac{x^3 + 3x^5 + 3x^4 + x^6}{3} - \\ & \frac{x^4+4x^5+6x^6 + 4x^7 + x^8}{4} + \frac{x^5 + 5x^6 + 10x^7 + 10x^8 + 5x^9 + x^{10} }{5} - \ldots \end{split} \end{equation*}\]

Bringing together the coefficients of $x,x^2, x^3, x^4, x^5 \ldots$,

\[\begin{equation*} \begin{split} \log (1+x+x^2) &= 1x + \left(1- \frac{1}{2}\right)x^2 + \left(-1 + \frac{1}{3}\right)x^3 + \left(-\frac{1}{2} + 1 -\frac{1}{4}\right)x^4 + \left(1-1 + \frac{1}{5}\right)x^5 \ldots\\ &= x + \frac{1}{2}x^2 - \frac{2}{3}x^3 + \frac{1}{4}x^4 + \frac{1}{5}x^5 \ldots \end{split} \end{equation*}\]

8.0.6 Question 5

Prove that $\sin ^{-1}x = x + \frac{x^3}{3!}+\frac{9x^5}{5!}+ \ldots$

Let $y= \sin^{-1} x$.

\[\begin{equation*} \begin{split} y_1 &= \frac{1}{\sqrt{1-x^2}}\\ (1-x^2)(y_1)^2 &= 1 \end{split} \end{equation*}\]

Differentiating w.r.t $x$,

\[\begin{equation*} \begin{split} (1-x^2)2y_1y_2 - 2x(y_1)^2 &= 0\\ (1-x^2)y_2 -xy_1 &= 0 \end{split} \end{equation*}\]

Differentiating $n$ times using Leibnitz’s theorem,

\[\begin{equation*} \begin{split} y_{n+2} (1-x^2) + ny_{n+1}(-2x) + \frac{n(n-1)}{2}y_n (-2) + 0 - (y_{n+1}x + ny_n) &= 0\\ (1-x^2)y_{n+2} - 2nxy_{n+1} - (n^2-n)y_n - xy_{n+1} - ny_n &= 0\\ (1-x^2)y_{n+2} - (2n+1)xy_{n+1} - n^2y_n &= 0 \end{split} \end{equation*}\]

Putting $x=0$,

\[\begin{equation*} \begin{split} (y_{n+2})_0 &= n^2(y_n)_0 \\ (y)_0 &= 0 \\ (y_1)_0 &= 1\\ (y_2)_0 &= 0\\ (y_3)_0 &= (y_1)_0 = 1\\ (y_4)_0 &= 4(y_2)_0 = 0\\ (y_5)_0 &= 9(y_3)_0 = 9 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

\[\begin{equation*} \begin{split} f(x) &= f(0) + xf'(0) + \frac{x^2}{2!}f''(0) + \frac{x^3}{3!}f'''(0) + \\ & \frac{x^4}{4!}f^4 (0) + \frac{x^5}{5!}f^5 (0) + \frac{x^6}{6!}f^6 (0) + \ldots\\ \sin^{-1} x &= 0 + x + 0 + \frac{x^3}{3!} \times 1 + 0 + \frac{x^5}{5!} \times 9 + \ldots\\ &= x + \frac{x^3}{3!} + \frac{9x^5}{5!} + \ldots \end{split} \end{equation*}\]

and hence show that $\cos ^{-1}x = \frac{\pi}{2}-x - \frac{x^3}{3!} - \ldots$

From the formula on inverse sum identities, we know that,

\[\begin{equation*} \begin{split} \sin^{-1} x + \cos^{-1} x &= \frac{\pi}{2}, \text{ or}\\ \cos^{-1} x &= \frac{\pi}{2} - \sin^{-1} x \end{split} \end{equation*}\]

We have already found the expansion for $\sin^{-1} x$, so,

\[\begin{equation*} \begin{split} \cos^{-1} x &= \frac{\pi}{2} - x - \frac{x^3}{3!} - \frac{9x^5}{5!} - \ldots \end{split} \end{equation*}\]

8.0.7 Question 6i

Show that $\frac{x}{e^x - 1} = 1 - \frac{1}{2}x + \frac{1}{12}x^2 - \frac{1}{720}x^4 + \ldots$

We know,

\[\begin{equation*} \begin{split} e^x &= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots \\ e^x - 1 &= x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots \end{split} \end{equation*}\]

So,

\[\begin{equation*} \begin{split} \frac{x}{e^x -1} &= \frac{x}{x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots}\\ \end{split} \tag{8.4} \end{equation*}\]

Let

\[\begin{equation*} \begin{split} \frac{x}{e^x -1} &= a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + a_5 x_5 + \ldots \\ \end{split} \tag{8.5} \end{equation*}\]

Equating (8.4) and (8.5),

\[\begin{equation*} \begin{split} \frac{x}{x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots} &= a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + a_5 x_5 + \ldots \\ x &= (a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + a_5 x_5 + \ldots)\\ & (x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots)\\ \end{split} \end{equation*}\]

Equating the coefficients of $x, x^2, x^3, x^4, x^5$,

\[\begin{equation*} \begin{split} a_0 &= 1 \\ \frac{a_0}{2!} + a_1 &= 0 & \Longrightarrow a_1 = -\frac{1}{2} \\ \frac{a_0}{3!} + \frac{a_1}{2!} + a_2 &= 0 & \Longrightarrow a_2 = \frac{1}{12}\\ \frac{a_0}{4!} + \frac{a_1}{3!}+ \frac{a_2}{2!} + a_3 &= 0 & \Longrightarrow a_3 = 0\\ \frac{a_0}{5!} + \frac{a_1}{4!} + \frac{a_2}{3!} + \frac{a_3}{2!}+ a_4 &= 0 & \Longrightarrow a_4 = -\frac{1}{720} \end{split} \end{equation*}\]

Substituting these values in (8.5), we get

\[\begin{equation*} \begin{split} \frac{x}{e^x -1} &= a_0 + a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 + a_5 x^5 + \ldots\\ &= 1 -\frac{1}{2}x + \frac{1}{12}x^2 + 0 - \frac{1}{720}x^4 + \ldots\\ &= 1 -\frac{1}{2}x + \frac{1}{12}x^2 - \frac{1}{720}x^4 + \ldots\\ \end{split} \end{equation*}\]

8.0.8 Question 6ii

Show that $e^{\sin^{-1}x} = 1 + x + \frac{x^2}{2!}+ \frac{2x^3}{3!}+\frac{5}{4!}x^4 + \ldots$

Let $y= e^{\sin^{-1}x}$.

Differentiating w.r.t $x$,

\[\begin{equation*} \begin{split} y_1 &= e^{\sin^{-1}x} \frac{1}{\sqrt{1-x^2}}\\ (1-x^2)(y_1)^2 &= y^2 \end{split} \end{equation*}\]

Differentiating again w.r.t $x$,

\[\begin{equation*} \begin{split} 2y_1 y_2 (1-x^2) - 2x(y_1)^2 &= 2yy_1\\ (1-x^2)y_2 - xy_1 &= y \end{split} \end{equation*}\]

Differentiating $n$ times using Leibnitz’s theorem,

\[\begin{equation*} \begin{split} y_{n+2}(1-x^2) - {}^{n}C_{1} 2xy_{n+1} - {}^{n}C_{2}2y_n - xy_{n+1} - {}^{n}C_{1}y_n &= y_n \\ (1-x^2)y_{n+2} - (2n+1)xy_{n+1} - (n^2 +1)y_n &= 0 \end{split} \end{equation*}\]

Putting $x=0$,

\[\begin{equation*} \begin{split} (y_{n+2})_0 &= (n^2 + 1)(y_n)_0 \\ (y)_0 &= e^0 = 1 \\ (y_1)_0 &= e^0 = 1\\ (y_2)_0 &= (y)_0 = 1\\ (y_3)_0 &= (1^2 + 1)(y_1)_0 = 2\\ (y_4)_0 &= (2^2 +1)(y_2)_0 = 5 \end{split} \end{equation*}\]

Using Maclaurin’s expansion for infinite series,

8.0.9 Question 6iii

If $y=e^{m\tan^{-1}x} = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \ldots$ show that

$(1+x^2)y_1 = my$

Given equation is $y=e^{m\tan^{-1}x}$. Differentiating w.r.t $x$,

\[\begin{equation*} \begin{split} y_1 &= e^{m\tan^{-1}x} \times m \times \frac{1}{1+x^2}\\ y_1 &= y \times m \times \frac{1}{1+x^2}\\ \end{split} \end{equation*}\]

\[\begin{equation} \begin{split} (1+x^2)y_1 = my \end{split} \tag{8.6} \end{equation}\]

$(n+1)a_{n+1} + (n-1)a_{n-1} = ma_n$

Differentiating equation (8.6) $n$ times using Leibnitz’s theorem, we have,

\[\begin{equation*} \begin{split} (1+x^2)y_{n+1} + ny_n \times 2x + \frac{n(n-1)}{2}y_{n-1} \times 2 + 0 &= my_n \end{split} \end{equation*}\]

\[\begin{equation*} \begin{split} (1+x^2)y_{n+1} + 2nxy_n + n(n-1)y_{n-1} &= my_n \end{split} \end{equation*}\]

\[\begin{equation*} \begin{split} (1+x^2)y_{n+1} + (2nx -m)y_n + n(n-1)y_{n-1} &= 0 \end{split} \tag{8.7} \end{equation*}\]

Differentiating equation (8.6) again w.r.t $x$,

\[\begin{equation*} \begin{split} (1+x^2)y_2 + 2xy_1 &= my_1\\ (1+x^2)y_2 + (2x-m)y_1 &= 0 \end{split} \end{equation*}\]

Also,

\[\begin{equation*} \begin{split} y &= a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \ldots & \Longrightarrow (y)_0 = a_0 \\ y_1 &= a_1 + 2a_2 x + 3a_3 x^2 + \ldots & \Longrightarrow (y_1)_0 = a_1 \\ y_2 &= 2a_2 + 6a_3 x + \ldots & \Longrightarrow (y_2)_0 = 2a_2 \\ y_3 &= 6a_3 + \ldots & \Longrightarrow (y_3)_0 = 6a_3 \end{split} \end{equation*}\]

Thus a pattern emerges, $(y_n)_0 = n! a_n$.

Putting $x=0$ in (8.7),

\[\begin{equation*} \begin{split} (y_{n+1})_0 -m(y_n)_0 + n(n-1) (y_{n-1})_0 &= 0\\ (n+1)! a_{n+1} - m n! a_n + n(n-1)(n-1)!a_{n-1} &= 0\\ n!(n+1) a_{n+1} - n! ma_n + (n-1)(n-1)! n a_{n-1} &= 0\\ n!(n+1) a_{n+1} - n! ma_n + n! (n-1)a_{n-1} &= 0\\ (n+1)a_{n+1} + (n-1)a_{n-1} &= ma_n \end{split} \end{equation*}\]

Also obtain the expansion of $e^{m\tan^{-1}x}$.

From the derivatives, we have

\[\begin{equation*} \begin{split} (y)_0 &= 1 = a_0\\ (y_1)_0 &= m(y)_0 = m = a_1\\ (y_2)_0 &= m(y_1)_0 = m^2 = 2a_2\\ \end{split} \end{equation*}\]

From $n^{\text{th}}$ derivative (8.7), putting $n= 2$,

\[\begin{equation*} \begin{split} (y_3)_0 &= m(y_2)_0 - 2(y_1)_0 \\ &= m \times m^2 - 2m \\ &= m(m^2 -2) = 6a_3 \end{split} \end{equation*}\]

So substituting values of $a_0, a_1, a_2, a_3, \ldots$ in $y= a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \ldots$, we have:

\[\begin{equation*} \begin{split} e^{m\tan^{-1}x} &= 1 + mx + \frac{m^2}{2!}x^2 + \frac{m(m^2-2)}{3!}x^3 + \ldots \end{split} \end{equation*}\]

8.0.10 Question 7

Show that the following functions cannot be expanded in Maclaurin’s infinite series.

$f(x) = \sqrt{x}$

\[\begin{equation*} \begin{split} f(x) &= \sqrt{x} & \Longrightarrow f(0) = 0\\ f'(x) &= \frac{1}{2\sqrt{x}} & \Longrightarrow f'(0) \text{ does not exist} \end{split} \end{equation*}\]

Since $f'(0)$ does not exist, so $\sqrt{x}$ cannot be expanded in Maclaurin’s infinite series.

$f(x) = x^{5/2}$

\[\begin{equation*} \begin{split} f(x) &= x^{5/2} & \Longrightarrow f(0) = 0\\ f'(x) &= \frac{5}{2} x^{3/2} & \Longrightarrow f'(0) = 0\\ f''(x) &= \frac{5}{2} \times \frac{3}{2} x^{1/2} & \Longrightarrow f''(0) = 0\\ f'''(x) &= \frac{5}{2} \times \frac{3}{2} \times \frac{1}{2\sqrt{x}} & \Longrightarrow f'''(0) \text{ does not exist} \end{split} \end{equation*}\]

Since $f'''(0)$ does not exist, so $x^{5/2}$ cannot be expanded in Maclaurin’s infinite series.