Chapter 11 Maxima and Minima-I

11.1 Exercise 6(i)

11.1.1 Question 1

Find the maximum and minimum values of the following functions

1. \(4x^3 -15x^2 +12x -2\)

Here,

\[\begin{equation*} \begin{split} f(x) &= 4x^3 -15x^2 +12x -2\\ f'(x) &= 12x^2 - 30x + 12\\ f''(x) &= 24x - 30 \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 12x^2 - 30x + 12 &= 0\\ 4x^2 - 10x + 4 &= 0\\ x &= \frac{10 \pm \sqrt{100 - 64}}{8} = 2 , \dfrac{1}{2}\\ \end{split} \end{equation*}\]

At \(x=2\), \(f''(2) = 18\) which is positive. At \(x=\frac{1}{2}\), \(f''\left(\frac{1}{2}\right)= -18\), which is negative.

Therefore, \(f(x)\) is maximum at \(x = \frac{1}{2}\) and minimum at \(x=2\). The respective values are \(f\left(\frac{1}{2}\right)= \frac{3}{4}\) and \(f(2) = -6\).

It is indeed revealed in the figure 11.1.

2. \(x+ \dfrac{1}{x}\)

Here,

\[\begin{equation*} \begin{split} f(x) &= x+ \dfrac{1}{x}\\ f'(x) &= 1 - \frac{1}{x^2}\\ f''(x) &= \frac{2}{x^3}\\ \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 1 - \frac{1}{x^2} &= 0\\ x &= \pm 1 \end{split} \end{equation*}\]

At \(x=1\), \(f''(1) = 2\) and at \(x=-1\), \(f''(-1) = -2\). So the function has maximum at \(x=-1, f(-1) = -2\) and minimum at \(x=1, f(1)=2\).

For visualisation, see 11.1.

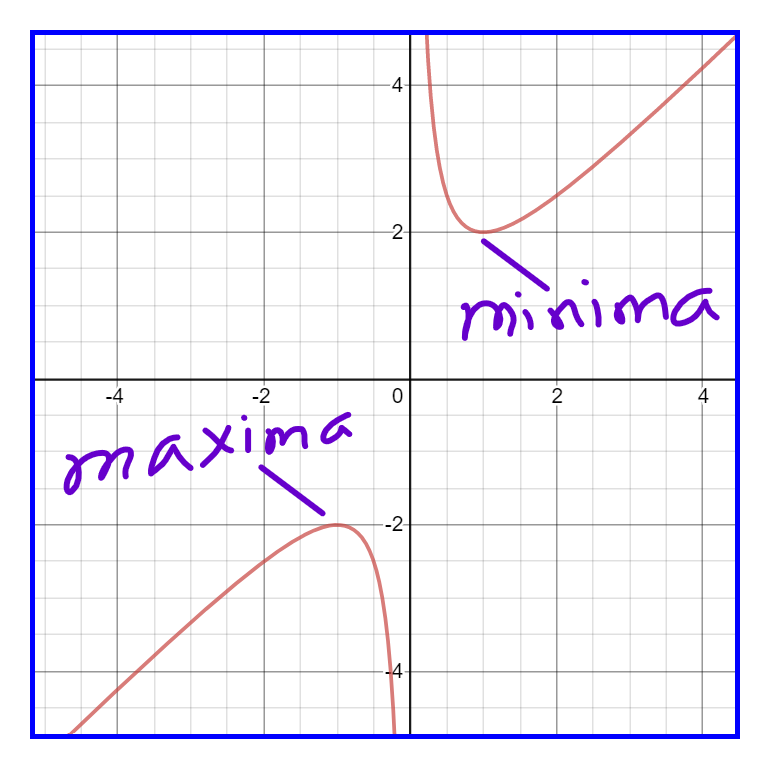
Figure 11.1: Plotting of function (a) \(4x^3 -15x^2 + 12 x -2\) showing maximum at \(x = \frac{1}{2}\) and minimum at \(x=2\) (b) \(x + \frac{1}{x}\) showing maximum at \(x=-1\) and minimum at \(x=1\).

3. \(x^3 - 3x^2 + 6x + 3\)

Here,

\[\begin{equation*} \begin{split} f(x) &= x^3 - 3x^2 + 6x + 3\\ f'(x) &= 3x^2 - 6x + 6\\ f''(x) &= 6x - 6 \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 3x^2 - 6x + 6 &= 0\\ x &= \dfrac{6 \pm \sqrt{36 - 72}}{6} \end{split} \end{equation*}\]

There are no real roots of \(f'(x) = 0\). In other words there are no points at the given curve where the slope is \(0\). So the given function has neither maximum nor minimum.

4. \(x^5 - 5x^4 + 5x^3 -1\)

Here,

\[\begin{equation*} \begin{split} f(x) &= x^5 - 5x^4 + 5x^3 -1\\ f'(x) &= 5x^4 - 20 x^3 + 15x^2\\ f''(x) &= 20x^3 - 60x^2 + 30x\\ \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 5x^4 - 20 x^3 + 15x^2 &= 0\\ x^2(x^2 -4x+3) &= 0\\ x &= 0, 1, 3 \end{split} \end{equation*}\]

So,

\(x\)	\(f''(x)\)
\(0\)	\(0\)
\(1\)	\(-10\), negative
\(3\)	\(90\), positive

Thus the function has maximum at \(x=1, f(1) = 0\) and minimum at \(x=3, f(3) = -28\). It has neither maximum nor minimum at \(x=0\).

The plotting reveals this graph:

22. \(\sin x\)

Here,

\[\begin{equation*} \begin{split} f(x) &= \sin x \\ f'(x) &= \cos x\\ f''(x) &= -\sin x \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ \cos x &= 0\\ x &= \frac{\pi}{2}, \frac{3\pi}{2} \\ &= \frac{\pi}{2}+ 2n\pi, \frac{3\pi}{2} + 2n\pi \\ \end{split} \end{equation*}\]

\(x\)	\(f''(x)\)
\(\frac{\pi}{2}+ 2n\pi\)	\(-1\), negative
\(\frac{3\pi}{2} + 2n\pi\)	\(1\), positive

So function has maximum value at \(x= \frac{\pi}{2} + 2n\pi\) which is \(1\) and minimum value at \(x= \frac{3\pi}{2} + 2n\pi\) which is \(-1\).

6. \(\cos x\)

Here,

\[\begin{equation*} \begin{split} f(x) &= \cos x\\ f'(x) &= -\sin x\\ f''(x) &= -\cos x \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ -\sin x &= 0\\ x &= 0, \pi \\ &= 2n\pi, \pi + 2n \pi \end{split} \end{equation*}\]

\(x\)	\(f''(x)\)
\(2n\pi\)	\(-1\), negative
\(\pi + 2n \pi\)	\(1\), positive

So the function has maximum at \(2n\pi\) which is \(1\) and minimum at \(\pi + 2n \pi\) which is \(-1\).

If \(f''(c) = f'''(c) = \ldots = f^{n-1}(c) = 0\) but \(f^n(c) \neq 0\) and if \(n\) is odd, \(x=c\) is neither a maximum nor a minimum point.

7. \(x^5\)

Here,

\[\begin{equation*} \begin{split} f(x) &= x^5\\ f'(x) &= 5x^4 \\ f''(x) &= 20x^3 \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ x &= 0 \end{split} \end{equation*}\]

So,

\[\begin{equation*} \begin{split} f''(0) &= f'''(0) = f^4(0) = 0\\ f^5(0) &= 5! \neq 0 \end{split} \end{equation*}\]

As the \(f^5(0) \neq 0\), where \(5\) is an odd number, the function has neither a maximum nor minimum at \(x=0\).

For graph see 11.2.

8. \(\sqrt{3} \sin x + 3\cos x\) at \(x=\dfrac{\pi}{6}\) only

Here,

\[\begin{equation*} \begin{split} f(x) &= \sqrt{3} \sin x + 3\cos x \\ f'(x) &= \sqrt{3} \cos x - 3\sin x \\ f''(x) &= -\sqrt{3} \sin x - 3\cos x \\ \end{split} \end{equation*}\]

So at given point \(x=\dfrac{\pi}{6}\),

\[\begin{equation*} \begin{split} f'\left(\dfrac{\pi}{6}\right) &= 0 \end{split} \end{equation*}\]

Thus slope at given point is \(0\). It can be either maximum or minimum. To test that, lets find the value of \(f''(x)\) at that point.

\[\begin{equation*} \begin{split} f''\left(\dfrac{\pi}{6}\right) &= -\sqrt{3} \sin \frac{\pi}{6} - 3\cos \frac{\pi}{6}\\ &= -\sqrt{3} \times \frac{1}{2} - 3 \times \frac{\sqrt{3}}{2}\\ &= -2\sqrt{3} \end{split} \end{equation*}\]

which is negative. Thus the given function \(\sqrt{3} \sin x + 3\cos x\) has local maximum at \(x=\dfrac{\pi}{6}\).

9. \(\sin x(1 + \cos x)\) at \(x = \dfrac{\pi}{3}\)

Here,

\[\begin{equation*} \begin{split} f(x) &= \sin x(1 + \cos x) \\ f'(x) &= (1+\cos x)\cos x - \sin^2 x\\ &= \cos x + \cos 2x \\ f''(x) &= -\sin x - 2\sin 2x \\ \end{split} \end{equation*}\]

So at given point \(x=\dfrac{\pi}{3}\),

\[\begin{equation*} \begin{split} f'\left(\dfrac{\pi}{3}\right) &= \cos \left(\dfrac{\pi}{3}\right) + \cos \left(\dfrac{2\pi}{3}\right)\\ &= \frac{1}{2} - \frac{1}{2} &= 0 \end{split} \end{equation*}\]

Thus slope at given point is \(0\). It can be either maximum or minimum. To test that, lets find the value of \(f''(x)\) at that point.

\[\begin{equation*} \begin{split} f''\left(\dfrac{\pi}{3}\right) &= -\sin \frac{\pi}{3} - 2\sin \frac{2\pi}{3}\\ &= \frac{-\sqrt{3}}{2} - \frac{2\sqrt{3}}{2}\\ &= \frac{-3\sqrt{3}}{2} \end{split} \end{equation*}\]

which is negative. Thus the given function \(\sin x(1 + \cos x)\) has local maximum at \(x=\dfrac{\pi}{3}\).

24. \(\dfrac{(x+1)(x+4)}{(x-1)(x-4)}\)

Plotting the graph shows,

Here,

\[\begin{equation*} \begin{split} f(x) &= \dfrac{(x+1)(x+4)}{(x-1)(x-4)}\\ f'(x) &= \dfrac{(x-1)(x-4)\dfrac{\mathrm{d}}{\mathrm{dx}} (x+1)(x+4) - (x+1)(x+4)\dfrac{\mathrm{d}}{\mathrm{dx}} (x-1)(x-4)}{(x-1)^2 (x-4)^2}\\ &= \dfrac{(x-1)(x-4)[(x+1) + (x+4)] - (x+1)(x+4)[(x-1) + (x-4)]}{(x-1)^2 (x-4)^2}\\ &= \dfrac{(x-1)(x-4)(2x+5) - (x+1)(x+4)(2x-5)}{(x-1)^2 (x-4)^2}\\ &= \dfrac{(x^2 - 5x +4)(2x+5) - (x^2 + 5x +4)(2x -5)}{(x-1)^2 (x-4)^2}\\ &= \dfrac{2x^3 - 10x^2 + 8x + 5x^2 - 25x + 20 -(2x^3 + 10x^2 + 8x - 5x^2 - 25x -20)}{(x-1)^2 (x-4)^2}\\ &= \dfrac{2x^3 - 2x^3 - 5x^2 - 5x^2 -17x + 17x +20 + 20}{(x-1)^2 (x-4)^2}\\ f'(x) &= \dfrac{-10x^2 + 40}{(x-1)^2 (x-4)^2}\\ \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ \dfrac{-10x^2 + 40}{(x-1)^2 (x-4)^2} &= 0\\ x^2 &= 4\\ x &= \pm 2 \end{split} \end{equation*}\]

Now lets find second derivative,

\[\begin{equation*} \begin{split} f''(x) &= \dfrac{(x-1)^2(x-4)^2 \times (-20x) - (40 -10 x^2)\dfrac{\mathrm{d}}{\mathrm{dx}} (x-1)^2(x-4)^2}{(x-1)^4(x-4)^4}\\ &= \dfrac{(x-1)^2(x-4)^2 \times (-20x) - (40 -10 x^2)\dfrac{\mathrm{d}}{\mathrm{dx}} \{(x-1)(x-4)\}^2 }{(x-1)^4(x-4)^4}\\ &= \dfrac{-20x(x-1)^2(x-4)^2 - (40 -10 x^2) \times 2(x-1)(x-4)\dfrac{\mathrm{d}}{\mathrm{dx}} (x-1)(x-4)}{(x-1)^4(x-4)^4}\\ &= \dfrac{-20x(x-1)^2(x-4)^2 - (40 -10 x^2) \times 2(x-1)(x-4)[(x-1) + (x-4)]}{(x-1)^4(x-4)^4}\\ &= \dfrac{-20x(x-1)^2(x-4)^2 - 10(4 -x^2) \times 2(x-1)(x-4)(2x-5)}{(x-1)^4(x-4)^4}\\ &= \dfrac{20(x-1)(x-4)\{-x(x-1)(x-4) - (4 -x^2)(2x-5)\}}{(x-1)^4(x-4)^4}\\ &= \dfrac{20(x-1)(x-4)\{-x^3 + 5x^2 - 4x - 8x + 20 + 2x^3 -5x^2\}}{(x-1)^4(x-4)^4}\\ &= \dfrac{20(x-1)(x-4)\{x^3 -12x + 20\}}{(x-1)^4(x-4)^4}\\ \end{split} \end{equation*}\]

For any values of \(x\), denominator is positive. So sign of numerator determines the sign.

At \(x=2\),

\[\begin{equation*} \begin{split} f''(2) &= \dfrac{(+)(-)(+)}{+} = - \end{split} \end{equation*}\]

At \(x=-2\),

\[\begin{equation*} \begin{split} f''(-2) &= \dfrac{(-)(-)(+)}{+} = + \end{split} \end{equation*}\]

So the function has maximum at \(x=2\) and minimum at \(x=-2\). The values respectively are \(f(2) = -9\) and \(f(-2) = -\frac{1}{9}\).

11.1.2 Question 2

Show that the following functions have neither maximum value nor minimum value

1. \(f(x)=x^3 - 9x^2 +28x -1\)

Here,

\[\begin{equation*} \begin{split} f(x) &= x^3 -9x^2 + 28x -1\\ f'(x) &= 3x^2 - 18x + 28\\ &= 3(x^2 -6x +9) + 1\\ &= 3(x-3)^2 + 1 \end{split} \end{equation*}\]

which cannot be zero for any value of \(x\). Hence \(f(x)\) has neither a maximum nor a minimum value.

2. \(f(x) = x^3 -6x^2 + 12x -3\)

The degree of equation is \(3\).

Here,

\[\begin{equation*} \begin{split} f(x) &= x^3 -6x^2 + 12x -3\\ f'(x) &= 3x^2 -12x + 12\\ f''(x) &= 6x -12\\ f'''(x) &= 6\\ \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 3x^2 -12x + 12 &= 0\\ 3(x-2)^2 &= 0\\ x &= 2 \end{split} \end{equation*}\]

So \(f''(2) = 0\) and \(f^3(2) \neq 0\). As \(3\) is odd, \(x=2\) is neither a maximum point nor a minimum point. See the above note.

For graph, see 11.2.

Figure 11.2: Plotting of function (a) \(x^5\) (b) \(x^3 -6x^2 +12x-3\).

11.1.3 Question 3

Given \(\dfrac{x}{2} + \dfrac{y}{3} = 1\), find the maximum value of \(xy\) and minimum value of \(x^2 + y^2\).

Given condition is,

\[\begin{equation*} \begin{split} \dfrac{x}{2} + \dfrac{y}{3} &= 1 \end{split} \tag{11.1} \end{equation*}\]

First part

We have to find maximum of \(xy\). Lets say \(f(x) = xy\). We have to find maximum value of \(f(x)\). So,

\[\begin{equation*} \begin{split} f(x) &= xy\\ &= x \left(\dfrac{6-3x}{2}\right)\\ &= \dfrac{1}{2}(6x-3x^2)\\ f'(x) &= 3-3x \end{split} \end{equation*}\]

To find extreme value of \(f(x)\),

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 3-3x &= 0\\ x &=1 \end{split} \end{equation*}\]

So we know extreme value of \(f(x)\) is at \(x=1\), but we need to know if its maximum or minimum. So,

\[\begin{equation*} \begin{split} f''(x) &= -3, \text{negative} \end{split} \end{equation*}\]

Thus \(f(x)\) has maximum at \(x=1\). Then plugging it into (11.1), we get \(y=\dfrac{3}{2}\). So maximum value of \(xy\) is \(\dfrac{3}{2}\).

Second part

We have to find minimum value of \(x^2 + y^2\). Lets say \(g(x) = x^2 + y^2\). From (11.1),

\[\begin{equation*} \begin{split} g(x) &= x^2 + y^2 = x^2 + \left(\dfrac{6-3x}{2}\right)^2 \\ &= x^2 + \dfrac{(6-3x)^2}{4}\\ g'(x) &= 2x + \dfrac{1}{4}\times 2 (6-3x)\times (-3)\\ g'(x) &= \dfrac{13x -18}{2}\\ g''(x) &= \dfrac{13}{2} \end{split} \end{equation*}\]

For the extreme value, \(g'(x) = 0\).

\[\begin{equation*} \begin{split} \dfrac{13x -18}{2} &= 0\\ x &= \dfrac{18}{13} \end{split} \end{equation*}\]

As the \(g''(x)\) is positive, the function \(g(x)\) has minimum at \(x= \frac{18}{13}\). Plugging into equation (11.1), \(y= \frac{12}{13}\).

Hence minimum value of \(g(x)\) is,

\[\begin{equation*} \begin{split} g(x) &= x^2 + y^2\\ &= \left(\dfrac{18}{13}\right)^2 + \left(\dfrac{12}{13}\right)^2\\ &= \dfrac{36}{13} \end{split} \end{equation*}\]

11.1.4 Question 4

Find the maxima and minima as well as the greatest and the least values of the function \(x^3 - 12x^2 + 45x\) in the interval \([0,7]\).

Here,

\[\begin{equation*} \begin{split} f(x) &= x^3 - 12x^2 + 45x \\ f'(x) &= 3x^2 -24x + 45\\ f''(x) &= 6x -24 \end{split} \end{equation*}\]

For maxima and minima,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ 3x^2 -24x + 45 &= 0\\ x^2 - 8x + 15 &= 0\\ x &= 3, 5 \end{split} \end{equation*}\]

Lets check value of \(f''(x)\) at these \(x\)-values.

\(x\)	\(f''(x)\)
\(3\)	\(f''(3) = -6\), negative
\(5\)	\(f''(5) = 6\), positive

So given function has maximum value at \(x=3, f(3) = 54\) and minimum at \(x=5, f(5) = 50\). Both values \(x=3,5\) lies in the given interval \([0,7]\).

Lets find the value of the function at the edges of the given interval,

\[\begin{equation*} \begin{split} f(0) &= 0\\ f(7) &= 7*7*7 - 12*49 + 45*7 = 70 \end{split} \end{equation*}\]

Thus least value is \(0\) and greatest value is \(70\).

For illustration, see the graph below:

Figure 11.3: Graph of \(x^3 -12x^2 + 45x\)

11.1.5 Question 5

1. Show that \(x^x\) is a minimum for \(x= \dfrac{1}{e}\) and that the maximum value of \(\left(\dfrac{1}{x}\right)^x\) is \(e^{1/e}\).

First part

Here,

\[\begin{equation*} \begin{split} f(x) &= y = x^x \\ \log y &= x \log x \\ \frac{1}{y}\frac{dy}{dx} &= \frac{x}{x} + \log x \\ \frac{1}{y}f'(x) &= 1 + \log x \\ f'(x) &= x^x(1+ \log x) \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ x^x(1+ \log x) &= 0\\ \log x &= -1\\ x &= e^{-1} \end{split} \end{equation*}\]

Differentiating again w.r.t. \(x\),

\[\begin{equation*} \begin{split} f''(x) &= (1 + \log x) \dfrac{\mathrm{d}}{\mathrm{dx}} x^x + x^x \dfrac{\mathrm{d}}{\mathrm{dx}} (1+ \log x) \\ &= (1+ \log x)f'(x) + \frac{x^x}{x}\\ f''(x) &= (1+ \log x)f'(x) + x^{x-1}\\ \end{split} \end{equation*}\]

At \(x=e^{-1}\),

\[\begin{equation*} \begin{split} f''(x) &= (1 + \log(e^{-1}))f'(e^{-1}) + \left(\dfrac{1}{e}\right)^{\frac{1}{e}-1}\\ &= 0 + \text{positive value} \\ &= \text{positive value} \end{split} \end{equation*}\]

Thus function \(x^x\) has minimum value at \(e^{-1}\). For graphics see 11.4.

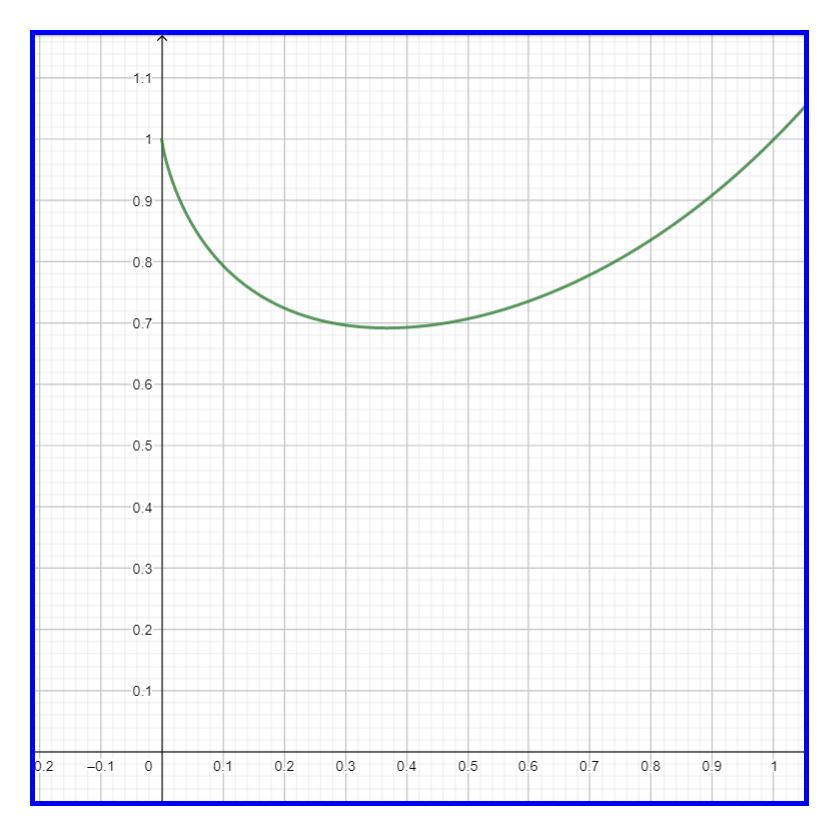
Figure 11.4: Plotting of function (a) \(x^x\) (b) Zoomed out to show minimum at \(x = e^{-1}\)

Second part

Here,

\[\begin{equation*} \begin{split} z &= g(x) = \left(\dfrac{1}{x}\right)^x \\ \log z = x \log \left(\frac{1}{x}\right)\\ \log z &= x(\log 1 - \log x) = -x \log x\\ \dfrac{1}{z}\dfrac{dz}{dx} &= -\left\{\frac{x}{x} + \log x\right\}\\ \end{split} \end{equation*}\]

\[\begin{equation} \begin{split} \dfrac{1}{z}g'(x) &= -\{1 + \log x\}\\ \end{split} \tag{11.2} \end{equation}\]

For extreme values,

\[\begin{equation*} \begin{split} g'(x) &= 0\\ -\{1 + \log x\} &= 0\\ \log x &= -1\\ x &= e^{-1} \end{split} \end{equation*}\]

Differentiating (11.2) w.r.t \(x\) to calculate second derivative,

\[\begin{equation*} \begin{split} \frac{1}{z}g''(x) - \frac{1}{z^2}(g'(x))^2 &= -\frac{1}{x}\\ \end{split} \end{equation*}\]

At \(x=e^{-1}\),

\[\begin{equation*} \begin{split} \frac{1}{z}g''(x) - 0 &= -\frac{1}{e^{-1}} = -e\\ g''(x) &= -ez = \text{negative}\\ \end{split} \end{equation*}\]

Thus \(g(x)\) has maximum value at \(e^{-1}\). The maximum value is,

\[\begin{equation*} \begin{split} \left(\dfrac{1}{x}\right)^x &= \left(\dfrac{1}{e^{-1}}\right)^{e^{-1}}\\ &= e^{\frac{1}{e}} \end{split} \end{equation*}\]

For illustration, see 11.5.

2. Test the function \(x^{1/x}\) for extreme values.

Here,

\[\begin{equation*} \begin{split} y &= f(x) = x^{1/x}\\ \log y &= \frac{1}{x}\log x \\ \frac{1}{y}\frac{dy}{dx} &= \frac{1}{x} \times \frac{1}{x} - \log x \times \frac{1}{x^2}\\ \frac{1}{y}\frac{dy}{dx} &= \frac{1}{x^2}(1 - \log x)\\ \frac{dy}{dx} &= \dfrac{x^{1/x}}{x^2}(1 - \log x)\\ f'(x) &= x^{\frac{1}{x}-2}(1 - \log x) \end{split} \end{equation*}\]

For extreme values,

\[\begin{equation*} \begin{split} f'(x) &= 0\\ x^{\frac{1}{x}-2}(1 - \log x) &= 0\\ 1 - \log x &= 0\\ x &= e \end{split} \end{equation*}\]

At a point immediate to the left or right of point \(x=e\), the value of \(x^{\frac{1}{x}-2}\) is positive, so the sign of \((1-\log x)\) determines the sign of \(f'(x)\). At a point immediate to the left of \(x=e\), \((1-\log x)\) is positive and at a point immediate to the right of \(x=e\), \((1-\log x)\) becomes negative.

So at point \(x=e\), slope of the curve changes from positive to negative, so the given function has maxima at point \(x=e\). The maximum value is,

\[\begin{equation*} \begin{split} f(e) &= e^{1/e} \end{split} \end{equation*}\]

For illustration, see 11.5.

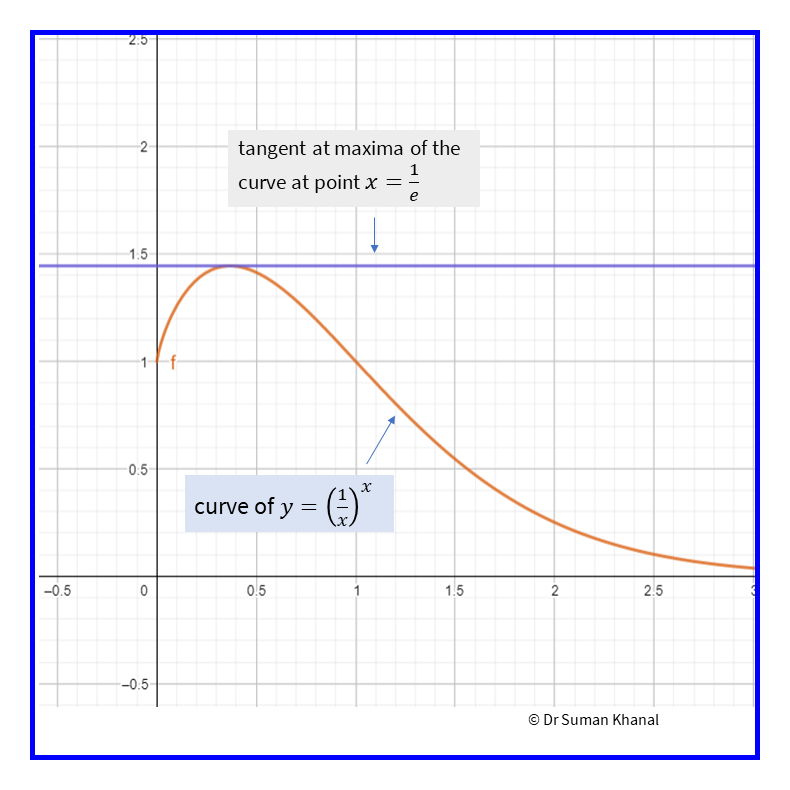
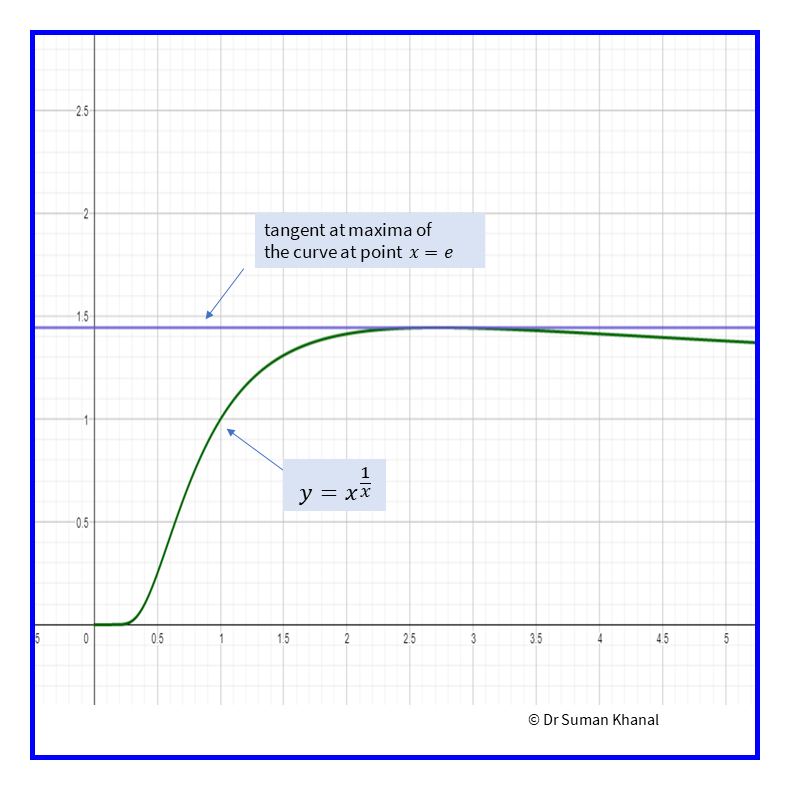
Figure 11.5: Plotting of function (a) \(\left(\frac{1}{x}\right)^x\) (b) \(x^{1/x}\)

11.1.6 Question 6

Show that of all rectangles of a given area, the square has the smallest perimeter.

Let \(x\) and \(y\) be dimensions of a rectangle of given area \(A\). So, \(A=xy\).

The perimeter is given by \(P = 2(x +y)\). We have to find value at which perimeter is smallest.

\[\begin{equation*} \begin{split} P &= 2(x + y)\\ &= 2\left(x + \frac{A}{x}\right)\\ P &= 2x + \frac{2A}{x}\\ \dfrac{dP}{dx} &= 2 - \dfrac{2A}{x^2} \end{split} \end{equation*}\]

To minimise perimeter,

\[\begin{equation*} \begin{split} \dfrac{dP}{dx} &= 0 \\ 2 - \dfrac{2A}{x^2} &= 0\\ x &= \sqrt{A} \end{split} \end{equation*}\]

as the dimension can only be positive. At a point immediate to the left of \(x = \sqrt{A}\), \(\frac{dP}{dx}\) is negative and at a point immediate to the right of \(x = \sqrt{A}\), \(\frac{dP}{dx}\) is positive. As the slope changes from negative to positive at \(x=\sqrt{A}\), the perimeter is minimum at this point.

We know,

\[\begin{equation*} \begin{split} A &= xy\\ y &= A/x\\ &= \sqrt{A} \end{split} \end{equation*}\]

Thus perimeter is minimum when \(x=\sqrt{A}\) and \(y=\sqrt{A}\). Both dimensions are equal. So, of all rectangles of a given area, the square has the smallest perimeter.

11.1.7 Question 7

Show that the largest rectangle with a given perimeter is a square.

Here, perimeter \(P\) is given and is a constant. We have to find maximum area \(A\) for a given perimeter.

So \(P= 2(x+y)\) for a rectangle. Similarly,

\[\begin{equation*} \begin{split} A &= xy\\ &= x\left(\frac{P}{2} - x\right)\\ A &= \frac{Px}{2} - x^2\\ \dfrac{dA}{dx} &= \frac{P}{2} - 2x\\ \dfrac{d^2A}{dx^2} &= -2\\ \end{split} \end{equation*}\]

For maximal value of \(A\),

\[\begin{equation*} \begin{split} \dfrac{dA}{dx} &= 0\\ \frac{P}{2} - 2x &= 0\\ x &= \frac{P}{4} \end{split} \end{equation*}\]

As second derivative \(\dfrac{d^2A}{dx^2}\) is negative, area is maximum at \(x = \frac{P}{4}\). And from \(P= 2(x+y)\), \(y= \frac{P}{4}\). So the dimensions are same i.e a square. Thus, the largest rectangle with a given perimeter is a square.

11.1.8 Question 8

Prove that the greatest rectangle that can be inscribed in the ellipse \(\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1\) has the area \(2ab\).

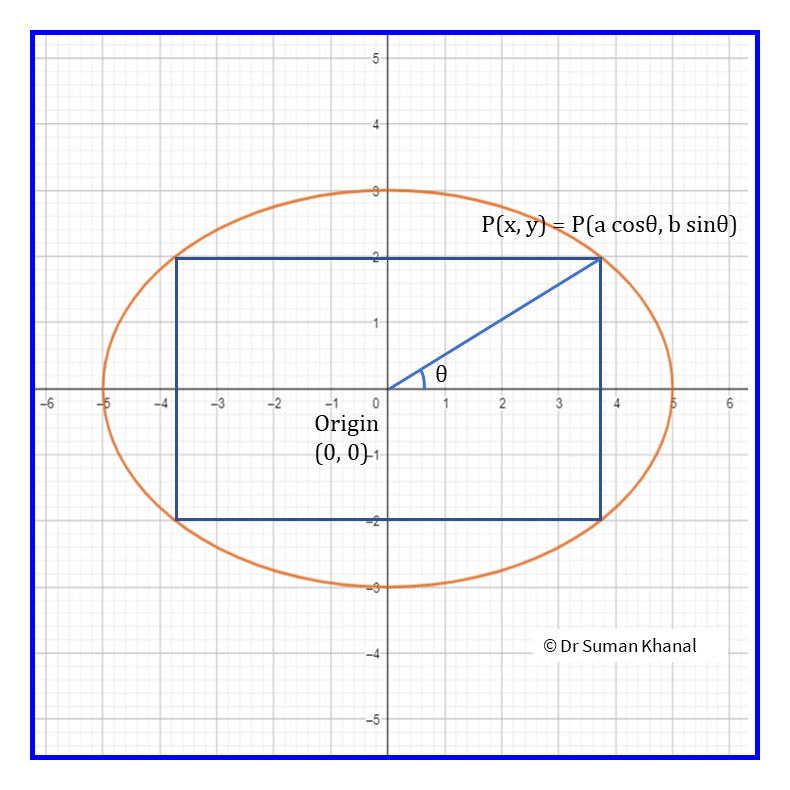
Figure 11.6: Parametric representation of ellipse with centre as origin

The parametric form for ellipse with equation \(\frac{x^2}{a^2} + \frac{x^2}{b^2} = 1\) is,

\[\begin{equation*} \begin{split} x &= a \cos \theta \\ y &= b \sin \theta \end{split} \end{equation*}\]

So from figure 11.6, the big rectangle incribed in ellipse is made of four small rectangles each with area of \(xy\). Total area \(A\) of big rectangle is,

\[\begin{equation*} \begin{split} A &= 4xy\\ &= 4 a \cos \theta \times b \sin \theta \\ &= 2ab \times 2\sin \theta \cos \theta \\ A &= 2ab \times \sin (2\theta) \end{split} \end{equation*}\]

For the area of rectangle to be maximum given \(a\) and \(b\) are fixed in a given ellipse,

\[\begin{equation*} \begin{split} \sin(2\theta) &= 1\\ 2 \theta &= \pi/2 \\ \theta &= \pi/4 \end{split} \end{equation*}\]

Thus maximum area of rectangle is \(A=2ab\) which happens when \(\theta = \pi/4\).

11.1.9 Question 9

A cylindrical tin close at both the ends and of a given capacity has to be constructed. Show that the amount of tin required will be a minimum when the height is equal to the diameter.

Figure 11.7: A cylidrical tin close at both ends with diameter D and height h

Here, capacity \(C\) of cylindrical tin is constant, diameter \(D\) and height \(h\) are variables. We have to minimise the amount of tin i.e surface area, required to construct cylinder close at both ends.

Capacity of tin (volume) is given by,

\[\begin{align} C &= \pi r^2 h = \dfrac{\pi h D^2}{4} \end{align}\]

Differentiating w.r.t height \(h\) (because we are minimising amount of tin w.r.t. height),

\[\begin{align} \dfrac{dC}{dh} &= \dfrac{\pi}{4} \left(D^2 + h \times 2D \times \dfrac{dD}{dh}\right) \\ 0 &= \dfrac{\pi}{4}\left(D^2 + 2hD\dfrac{dD}{dh}\right)\\ \dfrac{dD}{dh} &= -\dfrac{D}{2h} \tag{11.3} \end{align}\]

The amount of tin \(A\) required to build cylinder close at both ends is given by,

\[\begin{equation*} \begin{split} A &= 2\pi rh + 2\pi r^2 = \pi h D + \dfrac{\pi D^2}{2}\\ \end{split} \end{equation*}\]

Differentiating w.r.t \(h\),

\[\begin{equation*} \begin{split} \dfrac{dA}{dh} &= \pi \left(D + h\dfrac{dD}{dh}\right) + \dfrac{\pi}{2} \times 2D \times \dfrac{dD}{dh}\\ \end{split} \end{equation*}\]

Substituting from equation (11.3),

\[\begin{align} \dfrac{dA}{dh} &= \pi \left(D - \dfrac{hD}{2h}\right) - \dfrac{\pi D^2}{2h} \notag \\ &= \pi D - \dfrac{\pi D}{2} - \dfrac{\pi D^2}{2h} \notag \\ \dfrac{dA}{dh} &= \dfrac{\pi D}{2}\left(1-\dfrac{D}{h}\right) \tag{11.4} \end{align}\]

To find minima or maxima for amount of tin \(A\) w.r.t \(h\),

\[\begin{equation*} \begin{split} \dfrac{dA}{dh} &= 0\\ \dfrac{\pi D}{2}\left(1-\dfrac{D}{h}\right)\\ h &= D \end{split} \end{equation*}\]

From equation (11.4), at a point immediate to the left of \(h=D\), \(\dfrac{dA}{dh}\) is negative and at a point immediate to the right of \(h=D\), \(\dfrac{dA}{dh}\) is positive. So the slope \(\dfrac{dA}{dh}\) changes sign from negative to positive. The area \(A\) therefore has minimum at \(h=D\).

Thus when height is equal to the diameter, the amount of tin required will be a minimum.

11.1.10 Question 10

A square piece of tin of side \(18\) cm is to be made into a box without lid, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is maximum possible?

The given condition is reflected in the figure 11.8.

Figure 11.8: Square tin of \(18\) cm with a square of side \(x\) cut from each corner.

The volume of box \(V\) after cutting a square from each corner is given by (from the figure 11.8),

\[\begin{equation*} \begin{split} V &= \text{length} \times \text{breadth} \times \text{height}\\ &= (18-2x)(18-2x) \times x\\ &= 4x(81 - 18x + x^2)\\ V &= 4(x^3 - 18x^2 + 81x) \\ \dfrac{dV}{dx} &= 4(3x^2 - 36x + 81)\\ \dfrac{dV}{dx} &= 12(x^2 - 12x + 27)\\ \end{split} \end{equation*}\]

To maximise the volume \(V\) w.r.t \(x\),

\[\begin{equation*} \begin{split} \dfrac{dV}{dx} &= 0\\ 12(x^2 - 12x + 27) &= 0\\ x &= 3, 9 \end{split} \end{equation*}\]

Also,

\[\begin{equation*} \begin{split} \dfrac{d^2V}{dx^2} &= 12(2x -12)\\ \end{split} \end{equation*}\]

For \(x=3\), \(\dfrac{d^2V}{dx^2}\) is negative and for \(x=9\), \(\dfrac{d^2V}{dx^2}\) is positive. Thus, volume of box is maximum when \(x=3\) cm.