Chapter 13 Asymptotes-I

• Total number of asymptotes cannot exceed the highest degree of the equation.
• It is not necessary that all the curves have asymptotes.
• If a curve of nth degree has n asymptotes, then they cut the curve in n(n−2) points.

Tips on finding vertical and horizontal asymptotes can be found here.

13.1 Exercise 7

13.1.1 Question 1

Find the asymptotes of the curves

1. y=x(x−1)2(x−2)

Here, y→∞, when x→1.

Also, y→∞, when x→2, y→0 when x→∞.

So, there are three asymptotes.

x=1x=2y=0

2. y=x2x2+1

The equation is of degree 3. Here x3 is absent, so asymptotes parallel to x-axis is obtained by equating to zero the coefficients of highest degree term in x.

y−1=0y=1

Also y3 is absent, so asymptotes parallel to y-axis is obtained by equating to zero the coefficients of highest degree term in y.

x2+1=0

This doesn’t have real roots. So y=1 is the only asymptote.

In other words, there is no value of x such that y→∞. So, the equation doesn’t have vertical asymptote, horizontal asymptote only despite the degree of equation being 3.

3. y=4x2+4x−3x2−4x+3

The equation can be written as y=(2x+3)(2x−1)(x−1)(x−3).

Here, y→∞, when x→1, y→∞, when x→3 and y→4, when x→∞.

So asymptotes are,

x=1x=3y=4

4. y=x2+2x−1x

The function is a rational function and is improper. Trying to reduce fraction reveal difficult to manipulate roots of the numerator. So, no attempt is being made to reduce it further.

Here, y→∞, when x→0.

Also, y→∞, when x→∞. Hence, there is no asymptote parallel to x-axis.

To obtain oblique asymptote of form y=mx+c, we know,

m=lim

Also,

\begin{equation*} \begin{split} c &= \lim_{x \to \infty} (y - mx)\\ &= \lim_{x \to \infty} (y - x)\\ &= \lim_{x \to \infty} \left(\dfrac{x^2 + 2x -1}{x} - x\right)\\ &= \lim_{x \to \infty} \left(\dfrac{x^2 + 2x -1 -x^2}{x}\right)\\ &= \lim_{x \to \infty} \left(2 -\dfrac{1}{x}\right)\\ c &= 2 \end{split} \end{equation*}

The oblique asymptote is thus y = x+2.

All symptotes of the given equation are thus,

\begin{equation*} \begin{split} x &= 0\\ y &= x +2 \end{split} \end{equation*}

22. y = \dfrac{2x -3}{x^2 - 3x + 2}

The equation has degree 3. So it can have maximum of three asymptotes. It can be written as y = \dfrac{2x-3}{(x-1)(x-2)}.

Here, y \rightarrow \infty, when x \rightarrow 1 and x \rightarrow 2. Also y \rightarrow 0, when x \rightarrow \infty. It cannot have more than 3 asymptotes because the degree is 3. No need to proceed further. Thus the asymptotes are,

\begin{equation*} \begin{split} x &= 0\\ x &= 1\\ x &= 2 \end{split} \end{equation*}

6. y = \dfrac{(x+2)^2 (x-3)}{x-1}

Here, y \rightarrow \infty, when x \rightarrow 1.

Also, y \rightarrow \infty, when x \rightarrow \infty. So no asymptotes parallel to x-axis.

To find oblique asymptote,

\begin{equation*} \begin{split} m &= \lim_{x \to \infty} \dfrac{y}{x}\\ m &= \lim_{x \to \infty} \dfrac{\dfrac{x^3 + x^2 - 8x -12}{x-1}}{x}\\ &= \lim_{x \to \infty} \left(\dfrac{x^2 + x-8 - \frac{12}{x}}{x -1}\right)\\ &= \lim_{x \to \infty} \left(\dfrac{x + 1 - \frac{8}{x}- \frac{12}{x^2}}{1 - \frac{1}{x}}\right)\\ &= \infty \end{split} \end{equation*}

Thus, m is infinite. So, it does not have oblique asymptote. The only asymptote is x=1.

7. y= \dfrac{x^2 + 1}{1 + x}

The equation can be written as y = 1 + x - \dfrac{2x}{1 + x}.

Here, y \rightarrow \infty, when x \rightarrow -1.

Also, y \rightarrow \infty, when x \rightarrow \infty, So, no asymptotes parallel to x-axis.

For oblique asymptote of form y = mx + c,

\begin{equation*} \begin{split} m &= \lim_{x \to \infty} \dfrac{y}{x}\\ m &= \lim_{x \to \infty} \left(\frac{1}{x} + 1 - \frac{2}{1+x}\right)\\ m &= 1\\ c &= \lim_{x \to \infty} (y - mx)\\ &= \lim_{x \to \infty} (y - x)\\ &= \lim_{x \to \infty} \left(1 - \frac{2x}{1+x}\right)\\ &= -1 \end{split} \end{equation*}

Oblique asymptote is therefore y = x -1.

So all asymptotes of the equation are,

\begin{equation*} \begin{split} x + 1 &= 0\\ y &= x-1 \end{split} \end{equation*}

8. y = \dfrac{x}{x^2 -1}

It can be written as y = \dfrac{x}{(x+1)(x-1)}.

Here, y \rightarrow \infty, when x \rightarrow 1 and x \rightarrow -1. Also, y \rightarrow 0, when x \rightarrow \infty.

The asymptotes are thus,

\begin{equation*} \begin{split} x &= \pm 1\\ y &= 0 \end{split} \end{equation*}

9. (x^2 + y^2)x - ay^2 = 0

The equation is of degree 3. Here y^3 is absent, so asymptotes parallel to y-axis is obtained by equating the coefficients of highest degree of y to zero.

\begin{equation*} \begin{split} x - a &= 0\\ x &= a \end{split} \end{equation*}

We expect two more asymptotes. Let y = mx +c be the equation of asymptote.

Put x= 1, y=m,

\begin{equation*} \begin{split} \phi_3(m) &= 1 + m^2 \\ {\phi'}_3(m) &= 2m\\ \phi_2(m) &= -am^2 \end{split} \end{equation*}

Putting,

\begin{equation*} \begin{split} \phi_3(m) &= 0\\ 1 + m^2 &= 0\\ \end{split} \end{equation*}

m does not have real roots. So the equation does not have other asymptotes.

24. x^3 -y^3 = 3ax^2

The degree of equation is 3.

The equation does not have asymptotes parallel to x-axis and y-axis because the coefficients of x^3 and y^3 are constants.

Let y = mx +c be the oblique asymptotes to the curve. Putting x= 1, y= m,

\begin{equation*} \begin{split} \phi_3(m) &= 1 -m^3 \\ {\phi'}_3(m) &= -3m^2 \\ \phi_2(m) &= -3a \end{split} \end{equation*}

To find value of m,

\begin{equation*} \begin{split} \phi_3(m) &= 0 \\ 1 -m^3 &= 0\\ m &= 1 \end{split} \end{equation*}

Now,

\begin{equation*} \begin{split} c &= - \dfrac{\phi_2(m)}{{\phi'}_3(m)}\\ &= -\dfrac{-3a}{-3m^2}\\ c &= -a \end{split} \end{equation*}

So the equation of asymptote is y = x-a.

11. xy^2 - a^2(x-a) = 0

Degree of equation is 3. Here, x^3 is absent, so asymptotes parallel to x-axis are given by,

\begin{equation*} \begin{split} y^2 - a^2 &= 0\\ y &= \pm a \end{split} \end{equation*}

Here y^3 is also absent, so asymptote parallel to y-axis is,

\begin{equation*} \begin{split} x &= 0 \end{split} \end{equation*}

The asymptotes are thus,

\begin{equation*} \begin{split} x &= 0\\ y &= \pm a \end{split} \end{equation*}

12. (y-a)^2(x^2 - a^2) = x^4 + a^4

The equation can be written as (y-a)^2 = x^2 -a^2 + \dfrac{2x^2 a^2}{x^2 -a^2}.

Here, y \rightarrow \infty, when x \rightarrow \pm a.

Also, y \rightarrow \infty, when x \rightarrow \infty. So, no asymptotes parallel to x-axis.

Degree of equation is 4. We expect 4 asymptotes. Let y = mx +c be the equation of the remaining asymptotes.

Putting x=1, y=m,

\begin{equation*} \begin{split} \phi_4(m) &= m^2 -1\\ {\phi'}_4(m) &= 2m \\ \phi_3(m) &= -2am \end{split} \end{equation*}

For finding value of m,

\begin{equation*} \begin{split} \phi_4(m) &= 0\\ m^2 -1 &= 0\\ m &= \pm 1 \end{split} \end{equation*}

For finding value of c,

\begin{equation*} \begin{split} c &= - \dfrac{\phi_3(m)}{{\phi'}_4(m)} \\ &= \dfrac{2am}{2m} = a \end{split} \end{equation*}

Thus rest of the asymptotes are y \pm x = a. Thus the given equation has 4 asymptotes.

13. y(y-1)^2 - x^2y = 0

Degree of equation is 3.

Let y = mx +c be the equation of the asymptotes.

Putting x=1, y=m,

\begin{equation*} \begin{split} \phi_3(m) &= m^3 -m \\ {\phi'}_3(m) &= 3m^2 -1\\ \phi_2(m) &= -2m^2 \end{split} \end{equation*}

Finding value of m,

\begin{equation*} \begin{split} \phi_3(m) &= 0\\ m^3 -m &= 0\\ m(m^2 -1) &= 0\\ m &= 0, \pm 1 \end{split} \end{equation*}

For finding c,

\begin{equation*} \begin{split} c &= - \dfrac{\phi_2(m)}{{\phi'}_3(m)}\\ c &= \dfrac{2m^2}{3m^2 -1} \end{split} \end{equation*}

Now,

m	c
0	0
1	1
-1	1

The equation of the asymptotes are,

\begin{equation*} \begin{split} y &= 0 \\ y \pm x &= 1 \end{split} \end{equation*}

14. x^3 + y^3 = 3axy

The degree of equation is 3.

The coefficient of x^3 is 1 which is constant, so there are no asymptotes parallel to x-axis. Also, the coefficient of y^3 is 1 which is constant, so no asymptotes parallel to y-axis.

Let y=mx + c be the equation of the asymptotes. Then,

\begin{equation*} \begin{split} \phi_3(m) &= 1 + m^3 \\ {\phi'}_3(m) = 3m^2 \\ \phi_2(m) &= -3am \end{split} \end{equation*}

To find the value of m,

\begin{equation*} \begin{split} \phi_3(m) &= 0\\ 1 + m^3 &= 0\\ (1+m)(m^2 - m+1) &= 0\\ m &= -1 \text{ and two imaginary roots}\\ \end{split} \end{equation*}

Asymptote does not exist for imaginary values, so we consider only m=-1.

For c,

\begin{equation*} \begin{split} c &= - \dfrac{\phi_2(m)}{{\phi'}_3(m)}\\ &= \dfrac{3am}{3m^2}\\ &= \dfrac{a}{m} = -a \end{split} \end{equation*}

The asymptote is thus,

\begin{equation*} \begin{split} y + x + a &= 0 \end{split} \end{equation*}

13.1.2 Question 2

Determine the relative positions of the curves and the asymptotes in question number 1 [ii, iv, v] above.

1 ii.

For y=\dfrac{x^2}{x^2 + 1}, the only asymptote is y=1.

\begin{equation*} \begin{split} \lim (y-1) &= \lim \left(\dfrac{x^2}{x^2 + 1} - 1\right)\\ &= \lim \left(-\dfrac{1}{x^2 + 1}\right) \\ \end{split} \end{equation*}

When x \rightarrow +\infty, y-1 \rightarrow 0 through values less than 0 i.e negative values and when x \rightarrow -\infty, y-1 \rightarrow 0 through values less than 0 i.e negative values.

The curve thus approaches the asymptote y=1 from below both when x \rightarrow +\infty and x \rightarrow -\infty.

See the figure below.

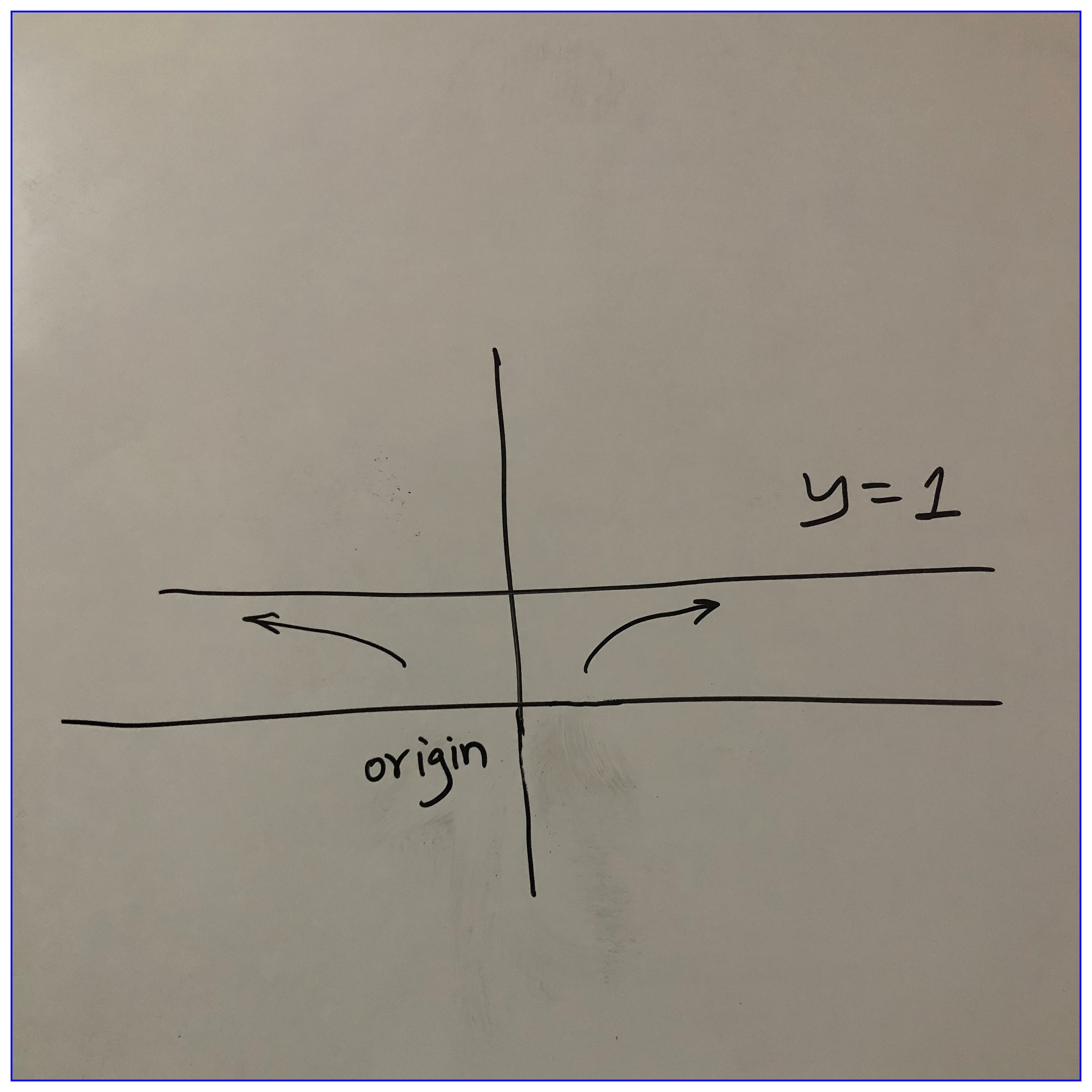
Figure 13.1: Curve and asymptote of \dfrac{x^2}{x^2 + 1}

1 iv.

For y = \dfrac{x^2 + 2x -1}{x}, the asymptotes are x=0 and y=x+2.

When x \rightarrow +0, y \rightarrow -\infty and when x \rightarrow -0, y \rightarrow +\infty.

When the curve approaches x=0 from positive side, the curve deflects toward -\infty and when approaches x=0 from negative side, the curve deflects toward +\infty.

Also,

\begin{equation*} \begin{split} \lim (y-x-2) &= \lim \left(\dfrac{x^2 + 2x -1}{x} - x- 2\right)\\ &= \lim \left(-\dfrac{1}{x}\right) \end{split} \end{equation*}

When x \rightarrow +\infty, y-x-2 \rightarrow -0 and x \rightarrow -\infty, y-x-2 \rightarrow +0.

Therefore, the curve approaches y-x-2=0, from below when x \rightarrow +\infty and from above when x \rightarrow -\infty. See 13.2.

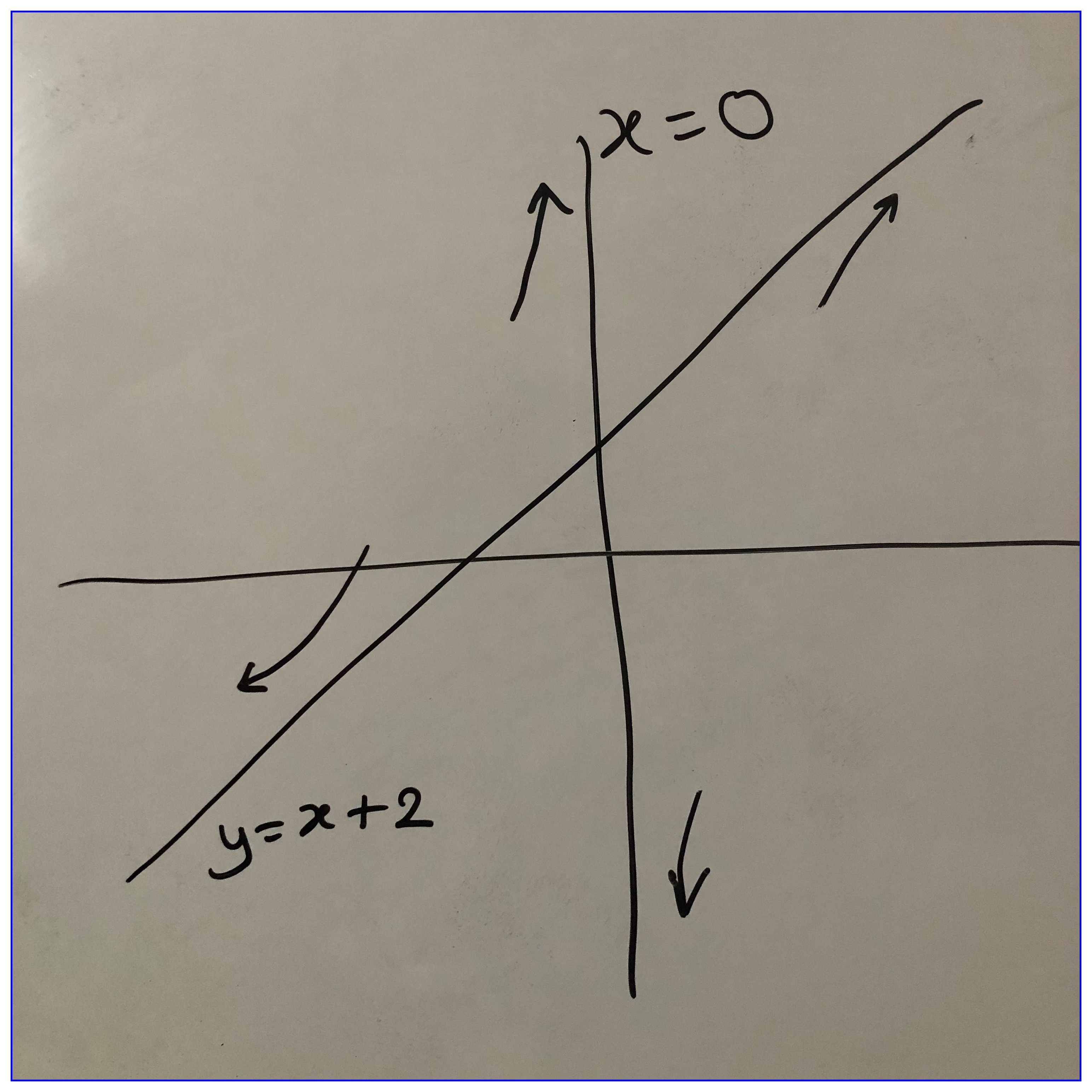
Figure 13.2: Curve and asymptotes of \dfrac{x^2 + 2x -1}{x}

1 v.

The asymptotes of y = \dfrac{2x -3}{x^2 - 3x + 2} are,

\begin{equation*} \begin{split} x &= 1\\ x &= 2\\ y &= 0 \end{split} \end{equation*}

When x=0, y =-\dfrac{3}{2}, so \left(0, -\dfrac{3}{2}\right) is the only crossing point here.

The equation can be written as \dfrac{2x -3}{(x-1)(x-2)}. So when,

\begin{equation*} \begin{split} x \rightarrow +\infty & \quad y \rightarrow +0 \\ x \rightarrow -\infty & \quad y \rightarrow -0 \\ x \rightarrow +1 & \quad y \rightarrow +\infty \\ x \rightarrow -1 & \quad y \rightarrow -\infty \\ x \rightarrow +2 & \quad y \rightarrow +\infty \\ x \rightarrow -2 & \quad y \rightarrow -\infty \\ \end{split} \end{equation*}

The relative position of the curve and the asymptotes is shown in 13.3.

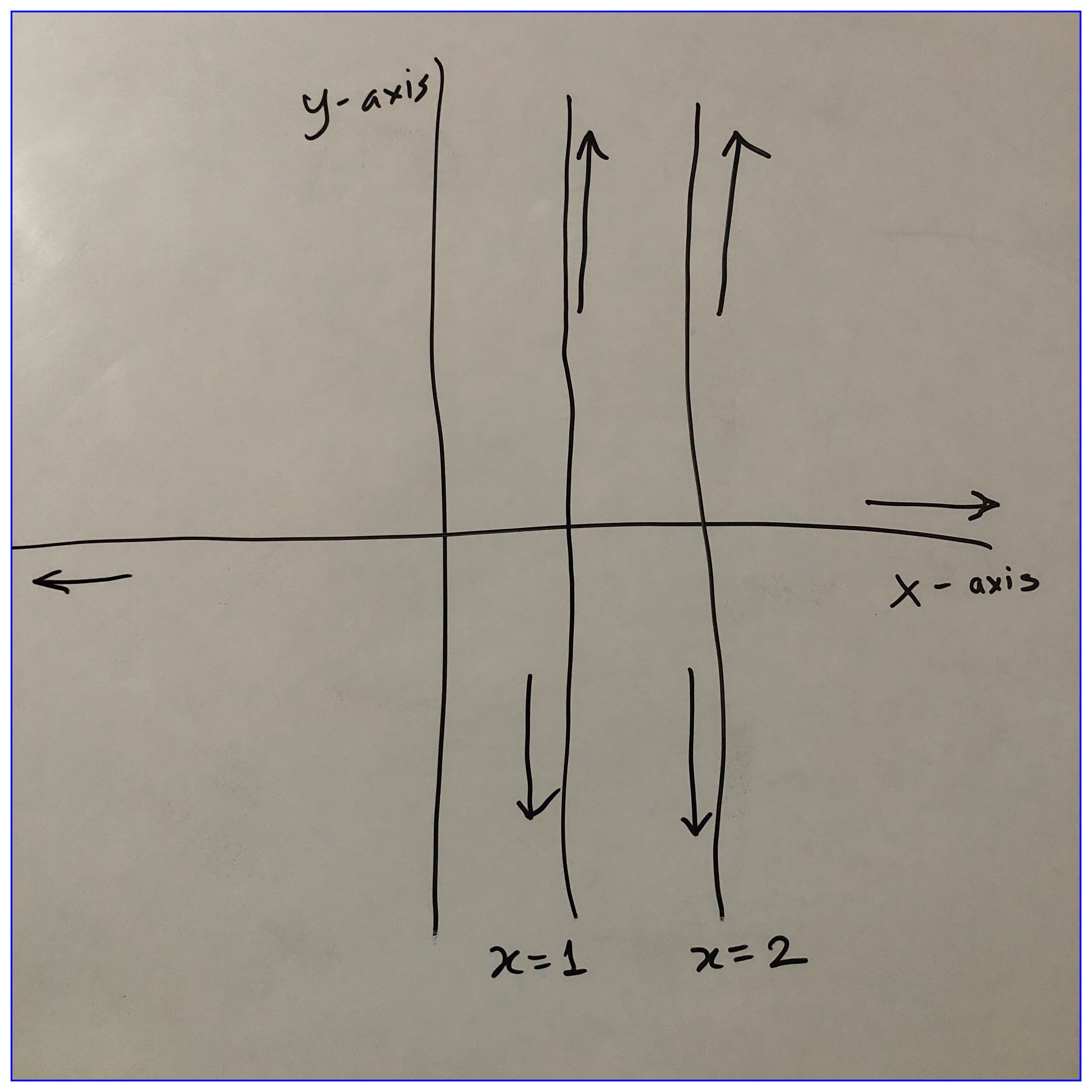
Figure 13.3: Curve and asymptotes of \dfrac{2x -3}{x^2 - 3x + 2}

13.1.3 Question 3

Find the asymptotes of the following curves

1. \dfrac{x^2}{a^2}- \dfrac{y^2}{b^2} = 1

The equation is of form F_2 - F_0 = 0.

\begin{equation*} \begin{split} \underbrace{\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2}}_{F_2} - \underbrace{1}_{F_0} &= 0 \end{split} \end{equation*}

So by the method of inspection,

\begin{equation*} \begin{split} F_2 &= 0\\ \dfrac{x^2}{a^2}- \dfrac{y^2}{b^2} &= 0\\ \left(\frac{x}{a} + \frac{y}{b}\right)\left(\frac{x}{a} - \frac{y}{b}\right) &= 0\\ \left(\frac{x}{a} + \frac{y}{b}\right) = 0, \left(\frac{x}{a} - \frac{y}{b}\right) &= 0 \end{split} \end{equation*}

Two linear factors are found which are different. The asymptotes are thus,

\begin{equation*} \begin{split} y \pm \frac{b}{a}x &= 0 \end{split} \end{equation*}

---

2. \dfrac{a^2}{x^2} + \dfrac{b^2}{y^2} = 1

The equation can be written as a^2y^2 + b^2 x^2 = x^2y^2.

The degree of equation is 4. There is no x^4. So asymptotes parallel to x-axis are obtained by equating the coefficients of highest degree term of x,

\begin{equation*} \begin{split} b^2 - y^2 &= 0\\ y &= \pm b \end{split} \end{equation*}

Similarly there is no y^4, so

\begin{equation*} \begin{split} a^2 - x^2 &= 0\\ x &= \pm a \end{split} \end{equation*}

Asymptotes are thus,

\begin{equation*} \begin{split} y &= \pm b \\ x &= \pm a \end{split} \end{equation*}

---

3. y^2 = \dfrac{(a-x)^2}{a^2 + x^2}x^2

The equation can also be written as x^2y^2 + a^2y^2 = (a-x)^2 x^2.

For no values of x, y \rightarrow \infty, so no horizontal asymptotes in this case. Degree of equation is 4, There is no y^4. Asymptotes parallel to y-axis are,

\begin{equation*} \begin{split} x^2 + a^2 &= 0 \end{split} \end{equation*}

x does not have real roots. So there are no asymptotes parallel to y-axis.

Let y= mx +c be the equation of asymptotes. Putting x=1 and y=m,

\begin{equation*} \begin{split} \phi_4(m) &= -1 + m^2 \\ {\phi'}_4(m) &= 2m\\ \phi_3(m) &= 2a \end{split} \end{equation*}

To find slope of the asymptotes,

\begin{equation*} \begin{split} \phi_4(m) &= 0\\ -1 + m^2 &= 0\\ m &= \pm 1 \end{split} \end{equation*}

For c,

\begin{equation*} \begin{split} c &= -\dfrac{\phi_3(m)}{{\phi'}_4(m)}\\ &= -\dfrac{2a}{2m}\\ &= - \dfrac{a}{m} \end{split} \end{equation*}

For m=1, \quad c=-a and for m=-1, \quad c =a. The equation of asymptotes are thus,

\begin{equation*} \begin{split} y &= x-a\\ y + x &= a \end{split} \end{equation*}

---

4. (a+x)^2(b^2 + x^2) = x^2y^2

Degree of equation is 4. No y^4, so

\begin{equation*} \begin{split} x^2 &= 0\\ x &= 0 \end{split} \end{equation*}

Let y = mx +c be the equation of asymptotes, putting x=1, y=m,

\begin{equation*} \begin{split} \phi_4(m) &= 1 - m^2\\ {\phi'}_4(m) &= -2m \\ \phi_3(m) &= 2a \end{split} \end{equation*}

The slope m of asymptotes are given by

\begin{equation*} \begin{split} \phi_4(m) &= 0\\ 1 - m^2 &= 0\\ m &= \pm 1 \end{split} \end{equation*}

For finding values of c,

\begin{equation*} \begin{split} c &= - \dfrac{\phi_3(m)}{{\phi'}_4(m)}\\ &= - \dfrac{2a}{-2m}\\ c &= \dfrac{a}{m} \end{split} \end{equation*}

For m =1, \quad c=a and for m = -1, \quad c =-a. Thus the asymptotes of the equation are

\begin{equation*} \begin{split} y &= x + a\\ y +x + a &= 0 \end{split} \end{equation*}

---

22. x^2y + xy^2 = a^3

The equation can be written as,

\begin{equation*} \begin{split} xy(x+y) - a^3 &= 0\\ \underbrace{xy(x+y)}_{F_3} - \underbrace{a^3}_{F_0} &= 0 \end{split} \end{equation*}

The F_3 has three non-repeating linear factors. The asymptotes thus can be obtained by method of inspection, equating F_3=0.

\begin{equation*} \begin{split} x &= 0\\ y &= 0\\ (x+y) &= 0 \end{split} \end{equation*}