Chapter 12 Maxima and Minima-II

12.1 Exercise 6(i)

12.1.1 Question 11

The sum of the surfaces of a cube and a sphere is given. When the sum of their volumes is least, show that the diameter of the sphere is equal to the edge of the cube.

Let the edge of cube be $a$ and diameter of sphere be $D$. The sum of surfaces of a cube and a sphere, $A$ is given and is constant.

Now, surface area of cube $S_C=6a^2$ and surface area of sphere $S_S=4\pi r^2=\pi D^2$.

Similarly, volume of cube $V_C=a^3$ and volume of sphere $V_S=\frac{4}{3}\pi r^3=\frac{\pi D^3}{6}$.

Total area of cube and sphere, A is given by,

$$\begin{array}{cc}A& =S_C+S_S\\ A& =6a^2+\pi D^2\\ 6a^2+\pi D^2& =A\end{array}$$

Differentiating w.r.t diameter $D$,

$$\begin{array}{cc}6\times 2a\frac{da}{dD}+2\pi D& =0,\text{as A is constant}\\ 3a\frac{da}{dD}& =-\frac{\pi D}{2}& \text{(12.1)}\end{array}$$

Also, total volume $V$ is given by,

$$\begin{array}{cc}V& =V_C+V_S\\ V& =a^3+\frac{\pi D^3}{6}& \text{(12.2)}\end{array}$$

To find the minimum total volume w.r.t $D$, we differentiate (12.2) w.r.t $D$ and plug $\frac{dV}{dD}=0$.

$$\begin{array}{cc}\frac{dV}{dD}& =3a^2\frac{da}{dD}+\frac{\pi }{6}3D^2\end{array}$$

Substituting from (12.1),

$$\begin{array}{cc}\frac{dV}{dD}& =-a\frac{\pi D}{2}+\frac{\pi D^2}{2}\\ \frac{dV}{dD}& =\frac{\pi D}{2}(D-a)& \text{(12.3)}\end{array}$$

To minimise or maximise total volume $V$ w.r.t diameter $D$,

$$\begin{array}{cc}\frac{dV}{dD}& =0\\ \frac{\pi D}{2}(D-a)& =0\\ D& =a\end{array}$$

From equation (12.3), at a point immediate to the left of $D=a$, $\frac{dV}{dD}$ is negative and at a point immediate to the right of $D=a$, $\frac{dV}{dD}$ is positive. So the slope $\frac{dV}{dD}$ changes sign from negative to positive. The total volume $V$ therefore has minimum at $D=a$.

Thus, when the sum of their volumes is least, the diameter of the sphere $D$ is equal to the edge $a$ of the cube.

12.1.2 Question 12

Show that the semi-vertical angle of the cone of maximum volume and given slant height is ${\tan }^{-1}\sqrt{2}$.

Let the semi-vertical angle of the cone is $\theta$. See the cone in figure 12.1.

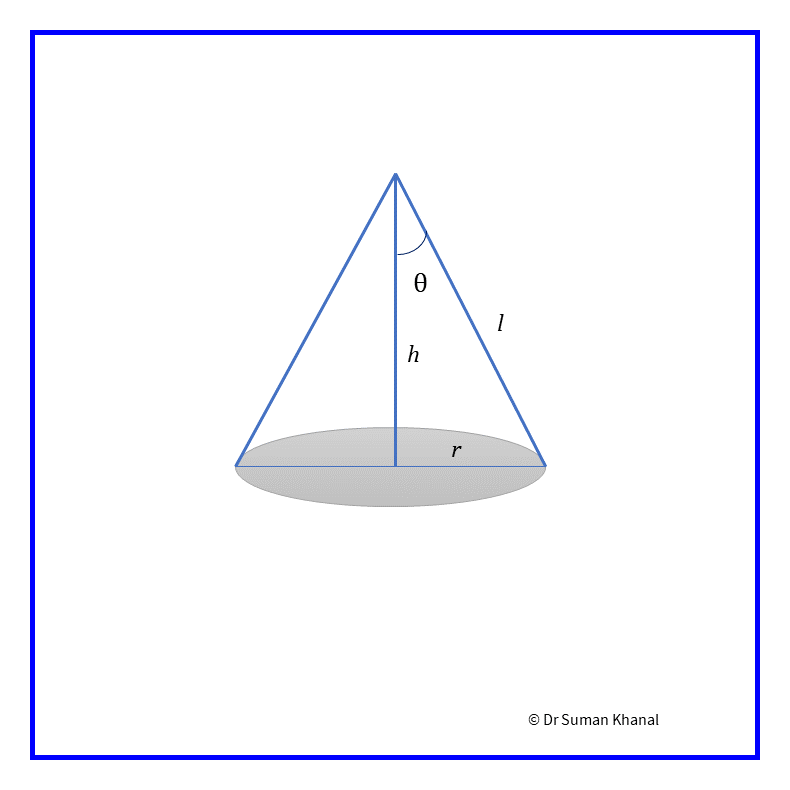
Figure 12.1: Illustrative cone

For the cone, only the slant height $l$ (constant) and angle is given. So from the figure,

$$\begin{array}{cc}r& =l\sin \theta \\ h& =l\cos \theta \end{array}$$

The volume $V$ of cone is given by,

$$\begin{array}{cc}V& =\frac{1}{3}\pi r^{2}h\\ & =\frac{1}{3}\pi l^2{\sin }^2\theta \times l\cos \theta \\ & =\frac{1}{6}\pi l^3\sin \theta \sin 2\theta \end{array}$$

We have to maximise the volume $V$ with respect to $\theta$, so differentiating w.r.t. $\theta$,

$$\begin{array}{cc}\frac{dV}{d\theta }& =\frac{\pi l^3}{6}(2\sin \theta \cos 2\theta +\cos \theta \sin 2\theta )\\ & =\frac{\pi l^3}{6}\left(2\sin \theta \right(2{\cos }^2\theta -1)+2{\cos }^2\theta \sin \theta )\\ & =\frac{\pi l^3}{6}2\sin \theta (2{\cos }^2\theta -1+{\cos }^2\theta )\\ & =\frac{\pi l^3}{3}\sin \theta (2{\cos }^2\theta -{\sin }^2\theta -{\cos }^2\theta +{\cos }^2\theta )\\ & =\frac{\pi l^3}{3}\sin \theta (2{\cos }^2\theta -{\sin }^2\theta )\\ & =\frac{\pi l^3}{3}\sin \theta (\sqrt{2}\cos \theta +\sin \theta )(\sqrt{2}\cos \theta -\sin \theta )\\ & =\frac{\pi l^3}{3}\sin \theta \cos \theta \frac{(\sqrt{2}\cos \theta +\sin \theta )}{\cos \theta }\frac{(\sqrt{2}\cos \theta -\sin \theta )}{\cos \theta }\cos \theta \\ \frac{dV}{d\theta }& =\frac{\pi l^3}{3}\sin \theta {\cos }^2\theta (\sqrt{2}+\tan \theta )(\sqrt{2}-\tan \theta )& \text{(12.4)}\end{array}$$

For maximising volume $V$ w.r.t $\theta$,

$$\begin{array}{cc}\frac{dV}{d\theta }& =0\\ \frac{\pi l^3}{3}\sin \theta {\cos }^2\theta (\sqrt{2}+\tan \theta )(\sqrt{2}-\tan \theta )& =0\\ \sin \theta {\cos }^2\theta (\sqrt{2}+\tan \theta )(\sqrt{2}-\tan \theta )& =0\end{array}$$

Condition	Value of $\theta$	Remarks
$\sin \theta =0$	$\theta =0$	Semivertical angle of cone can’t be $0$
${\cos }^2\theta =0$	$\theta ={90}^0$	Semivertical angle of cone can’t be ${90}^0$
$\sqrt{2}+\tan \theta =0$	$\tan \theta =-\sqrt{2}$	Angle of cone is an acute angle. For acute angle values, $\tan \theta$ cannot be negative.
$\sqrt{2}-\tan \theta =0$	$\tan \theta =\sqrt{2}$	Possible value

So at $\tan \theta =\sqrt{2}$ i.e $\theta ={\tan }^{-1}\sqrt{2}$, the volume of cone can be maximum or minimum.

For acute angle of cone, from equation (12.4), $\sin \theta$, ${\cos }^2\theta$, $\sqrt{2}+\tan \theta$ are positive. So the value of $\sqrt{2}-\tan \theta =0$ determines the sign of $\frac{dV}{d\theta }$.

Lets find the slope $\frac{dV}{d\theta }$ at immediate neighbourhood of $\theta ={\tan }^{-1}\sqrt{2}$.

$\theta$	$\tan \theta$	$\sqrt{2}-\tan \theta$	$\frac{dV}{d\theta }$
$\theta <{\tan }^{-1}\sqrt{2}$	$\tan \theta <\sqrt{2}$	positive	positive
$\theta >{\tan }^{-1}\sqrt{2}$	$\tan \theta >\sqrt{2}$	negative	negative

So at $\theta ={\tan }^{-1}\sqrt{2}$, the slope $\frac{dV}{d\theta }$ changes from positive to negative. Hence the volume of cone is maximum at this angle.

Easy solution

From figure 12.1, according to Pythagoras’ theorem,

$$\begin{array}{cc}{l}^2& =r^2+h^2\\ r^2& =l^2-h^2& \text{(12.5)}\end{array}$$

The volume of the cone $V$ is given by,

$$\begin{array}{cc}V& =\frac{1}{3}\pi r^{2}h\end{array}$$

Substituting from (12.5),

$$\begin{array}{cc}V& =\frac{1}{3}\pi r^{2}h\\ & =\frac{1}{3}\pi (l^2-h^2)h\\ V& =\frac{\pi }{3}(l^{2}h-h^3)\end{array}$$

Differentiating w.r.t $h$,

$$\begin{array}{cc}\frac{dV}{dh}& =\frac{\pi }{3}(l^2-3h^2)\\ \frac{d^{2}V}{d{h}^2}& =\frac{\pi }{3}(0-6h)=-\frac{6\pi h}{3}\end{array}$$

To maximise or minimise the volume $V$ w.r.t $h$,

$$\begin{array}{cc}\frac{\pi }{3}(l^2-3h^2)& =0\\ \sqrt{3}h& =l\\ h& =\frac{l}{\sqrt{3}}\end{array}$$

With $h=\frac{l}{\sqrt{3}}$, $\frac{d^{2}V}{d{h}^2}$ is negative. So at $h=\frac{l}{\sqrt{3}}$, volume of cone is maximum.

From equation (12.5),

$$\begin{array}{cc}r& =\sqrt{l^2-h^2}\\ & =\sqrt{l^2-\frac{l^2}{3}}\\ r& =\frac{\sqrt{2}l}{\sqrt{3}}\end{array}$$

We have to find $\theta$ in terms of $\tan$, so,

$$\begin{array}{cc}\tan \theta & =\frac{r}{h}\\ & =\frac{\frac{\sqrt{2}l}{\sqrt{3}}}{\frac{l}{\sqrt{3}}}\\ \tan \theta & =\sqrt{2}\\ \theta & ={\tan }^{-1}\sqrt{2}\end{array}$$

So at $\theta ={\tan }^{-1}\sqrt{2}$, the volume of cone is maximum.

12.1.3 Question 13

Find the surface of the right circular cylinder of greatest surface, which can be inscribed in a sphere of radius $r$.

A right circular cylinder is a cylinder whose base is a circle and whose elements are perpendicular to its base. For details, see here.

Figure 12.2: Cylinder of greatest surface inscribed in a sphere

From the figure, the total surface area of the cylinder is,

$$\begin{array}{cc}& =2\left(\text{area of the base}\right)+\left(\text{lateral surface area}\right)\\ & =2\pi y^2+2\pi y\left(2x\right)\end{array}$$

From the figure 12.2,

$$\begin{array}{cc}{x}^2+y^2& =r^2\\ y& =\sqrt{r^2-x^2}\end{array}$$

Now expressing the total surface area in terms of $x$ ($r$ is given and is a constant),

$$\begin{array}{cc}S\left(x\right)& =2\pi (r^2-x^2)+2\pi \left(\sqrt{r^2-x^2}\right)\left(2x\right)\\ & =2\pi (r^2-x^2)+2\pi \left(x\sqrt{r^2-x^2}\right)\\ S^{\prime }\left(x\right)& =0-4\pi x+4\pi [x\times \frac{1}{2\sqrt{r^2-x^2}}\times (-2x)+\sqrt{r^2-x^2}\times 1]\\ & =4\pi [-x-\frac{x^2}{\sqrt{r^2-x^2}}+\sqrt{r^2-x^2}]\\ & =4\pi \left[\frac{-x\sqrt{r^2-x^2}-x^2+r^2-x^2}{\sqrt{r^2-x^2}}\right]\\ S^{\prime }\left(x\right)& =4\pi \left[\frac{-x\sqrt{r^2-x^2}-2x^2+r^2}{\sqrt{r^2-x^2}}\right]\end{array}$$

To find maximum or minimum of surface area,

$$\begin{array}{cc}{S}^{\prime }\left(x\right)& =0\\ 4\pi \left[\frac{-x\sqrt{r^2-x^2}-2x^2+r^2}{\sqrt{r^2-x^2}}\right]& =0\\ x\sqrt{r^2-x^2}& =r^2-2x^2& \text{(12.6)}\end{array}$$

Squaring both sides,

$$\begin{array}{cc}{x}^2(r^2-x^2)& =(r^2-2x^2{)}^2\\ r^2{x}^2-x^4& =r^4-4r^2{x}^2+4x^4\\ 5x^4-5r^2{x}^2+r^4& =0& \text{(12.7)}\end{array}$$

This is a quadratic equation in $x^2$ i.e $5(x^2{)}^2-(5r^2)x^2+r^4=0$

Applying quadratic formula,

$$\begin{array}{cc}{x}^2& =\frac{5r^2\pm \sqrt{25r^4-20r^4}}{10}\\ & =\frac{5r^2\pm \sqrt{5}{r}^2}{10}\\ x^2& =\frac{5\pm \sqrt{5}}{10}{r}^2\end{array}$$

When we apply root with $+$ sign to (12.6), the left side is positive and the right side is negative. So we reject the root with $+$ sign. Thus

$$\begin{array}{c}x=r\sqrt{\frac{5-\sqrt{5}}{10}}\end{array}$$

Since $S\left(0\right)=S\left(r\right)=0$, the maximum surface area occurs at this value of $x$. Now we know,

$$\begin{array}{cc}{y}^2& =r^2-x^2\\ & =r^2-\frac{5\pm \sqrt{5}}{10}{r}^2\\ y^2& =\frac{5+\sqrt{5}}{10}{r}^2\\ y& =r\sqrt{\frac{5+\sqrt{5}}{10}},\text{dimension cannot be negative}\end{array}$$

The greatest surface area is then,

$$\begin{array}{cc}& =2\pi y^2+4\pi xy\\ & =2\pi \frac{5+\sqrt{5}}{10}{r}^2+4\pi \times r\sqrt{\frac{5-\sqrt{5}}{10}}\times r\sqrt{\frac{5+\sqrt{5}}{10}}\\ & =\pi r^2[2\times \frac{5+\sqrt{5}}{10}+4\times \frac{\sqrt{(5-\sqrt{5})(5+\sqrt{5})}}{10}]\\ & =\pi r^2[\frac{5+\sqrt{5}}{5}+\frac{2\sqrt{20}}{5}]\\ & =\pi r^2\left[\frac{5+\sqrt{5}+4\sqrt{5}}{5}\right]\\ & =\pi r^2\left[\frac{5+5\sqrt{5}}{5}\right]\end{array}$$

12.1.4 Question 14

Show that the radius of the right circular cylinder of greatest curve surface which can be inscribed in a given cone is half that of the cone.

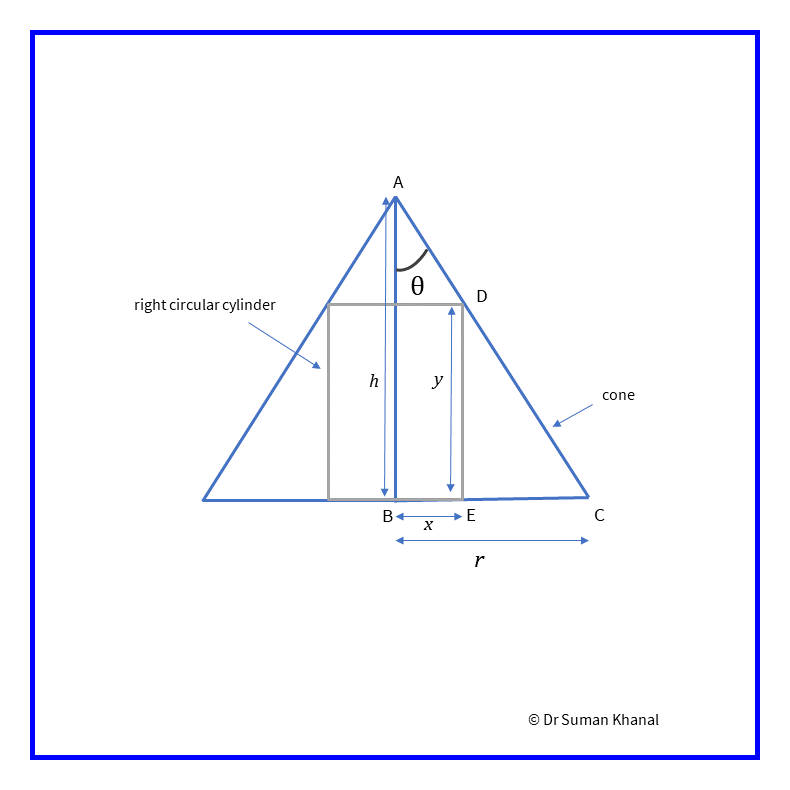
Figure 12.3: Side view of right circular cylinder inscribed in a cone

The given cone has height $h$ and radius $r$ which will be constant.

From figure 12.3, triangles $△ABC$ and $△DEC$ are similar triangles, so

$$\begin{array}{cc}\frac{y}{h}& =\frac{r-x}{r}\\ y& =\frac{h(r-x)}{r}& \text{(12.8)}\end{array}$$

The area of curve surface of cylinder is,

$$\begin{array}{cc}A& =2\pi xy\end{array}$$

Substituting from equation (12.8),

$$\begin{array}{cc}A& =2\pi x\frac{h(r-x)}{r}\\ & =\frac{2\pi h(rx-x^2)}{r}\\ \frac{dA}{dx}& =\frac{2\pi h}{r}(r-2x)\\ \frac{d^{2}A}{d{x}^2}& =\frac{2\pi h}{r}(-2)\text{, negative}\end{array}$$

To find maxima or minima of curve surface of cylinder w.r.t its radius $x$,

$$\begin{array}{cc}\frac{dA}{dx}& =0\\ \frac{2\pi h}{r}(r-2x)& =0\\ x& =\frac{r}{2}\end{array}$$

$\frac{d^{2}A}{d{x}^2}$ is negative. So at $x=\frac{r}{2}$, the curve surface area is maximum. Hence, the radius of the right circular cylinder of greatest curve surface which can be inscribed in a given cone is half that of the cone.

12.1.5 Question 15

Find the altitude of the right circular cylinder of maximum volume that can be inscribed in a given right circular cone of height $h$.

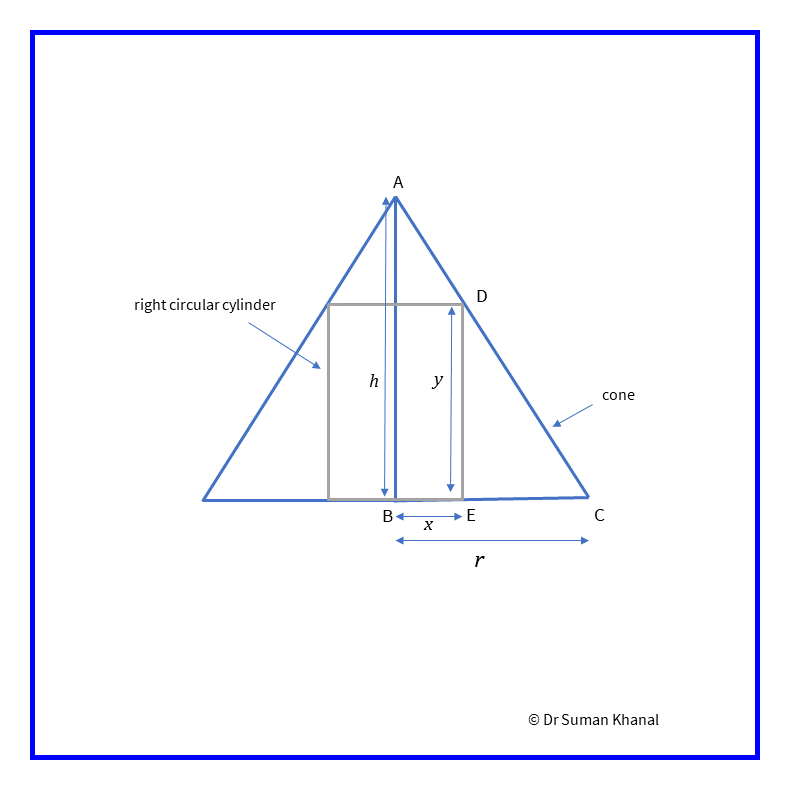
Figure 12.4: Side view of right circular cylinder inscribed within the cone

As per question, we have to find $y$ in the figure 12.4. For a given cone, $h$ and $r$ are constants.

From figure 12.4, triangles $△ABC$ and $△DEC$ are similar triangles, so

$$\begin{array}{cc}\frac{y}{h}& =\frac{r-x}{r}\\ y& =\frac{h(r-x)}{r}& \text{(12.9)}\end{array}$$

The volume of cylinder is,

$$\begin{array}{cc}V& =\pi x^{2}y\\ & =\pi x^2\frac{h(r-x)}{r}\\ V& =\frac{\pi h}{r}(r{x}^2-x^3)\\ \frac{dV}{dx}& =\frac{\pi h}{r}(2xr-3x^2)\\ \frac{d^{2}V}{d{x}^2}& =\frac{\pi h}{r}(2r-6x)\end{array}$$

For maxima or minima of cylinder volume w.r.t radius $x$ of cylinder,

$$\begin{array}{cc}\frac{dV}{dx}& =0\\ \frac{\pi h}{r}(2xr-3x^2)& =0\\ x& =\frac{2r}{3}\end{array}$$

At $x=\frac{2r}{3}$, $\frac{d^{2}V}{d{x}^2}$ is negative. So volume of cylinder is maximum when $x=\frac{2r}{3}$. Plugging value of $x$ into equation (12.9), we get $y=\frac{h}{3}$. Height of cylinder should be one-third of height of cone to have maximum volume.

12.1.6 Question 16

If $40$ square feet of sheet metal are to be used in the construction of an open tank with a square base, find the dimensions in order that its capacity is greatest.

Figure 12.5: Open tank with square base

The tank has no lid and base is square. So the dimensions of base will be $x$ and $x$ feet. The height of tank will be $y$ feet.

Available sheet of metal is $40$ square feet. The constructed tank will have area $A=x^2+4xy$.

So,

$$\begin{array}{cc}{x}^2+4xy& =40\\ xy& =\frac{40-x^2}{4}& \text{(12.10)}\end{array}$$

The volume of tank is,

$$\begin{array}{cc}V& =x^{2}y\end{array}$$

From equation (12.10),

$$\begin{array}{cc}V& =x\frac{40-x^2}{4}\\ & =\frac{1}{4}(40x-x^3)\\ \frac{dV}{dx}& =\frac{1}{4}(40-3x^2)\\ \frac{d^{2}V}{d{x}^2}& =\frac{1}{4}(-6x)\end{array}$$

To maximise the volume of tank w.r.t base width $x$,

$$\begin{array}{cc}\frac{dV}{dx}& =0\\ \frac{1}{4}(40-3x^2)& =0\\ x& =\sqrt{\frac{40}{3}},\text{cannot be negative}\end{array}$$

Plugging value of $x$ into equation (12.10), we get $y=\frac{1}{2}\sqrt{\frac{40}{3}}$. Thus the values are,

$$\begin{array}{cc}x& =\sqrt{\frac{40}{3}}\\ y& =\frac{1}{2}\sqrt{\frac{40}{3}}\end{array}$$

12.1.7 Question 17

The strength of a beam varies jointly as its breadth and the square of its depth. Find the dimensions of the strongest beam that can be cut from a circular wooden log of radius $a$.

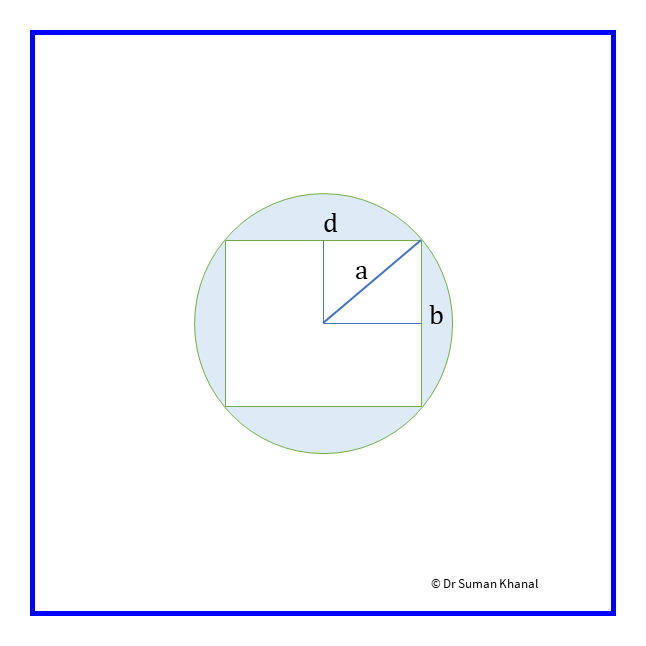
Figure 12.6: Beam cut out of circular wooden log, superior view

Let the beam has breadth $b$ and depth $d$. Then, from Pythagoras’ theorem,

$$\begin{array}{cc}{a}^2& =\frac{b^2}{4}+\frac{d^2}{4}\\ d^2=4a^2-b^2& & \text{(12.11)}\end{array}$$

The strength or power $P$ of beam varies as product of breadth and square of its depth, so

$$\begin{array}{cc}P& =b\times d^2\\ & =b(4a^2-b^2)\\ P& =4a^{2}b-b^3\\ \frac{dP}{db}& =4a^2-3b^2\\ \frac{d^{2}P}{d{b}^2}& =-6b,\text{negative}\end{array}$$

The beam strength is maximum or minimum with respect to beam breadth when,

$$\begin{array}{cc}\frac{dP}{db}& =0\\ 4a^2-3b^2& =0\\ b& =\frac{2a}{\sqrt{3}},\text{dimension cannot be negative}\end{array}$$

Putting value of $b$ in equation (12.11), we get $d=\frac{2\sqrt{2}a}{\sqrt{3}}$.

12.1.8 Question 18

A cone is circumscribed to a sphere of radius $r$, show that when the volume of the cone is least, its altitude is $4r$ and its semi-vertical angle is ${\sin }^{-1}\frac{1}{3}$.

The given condition is drawn in the following figure 12.7.

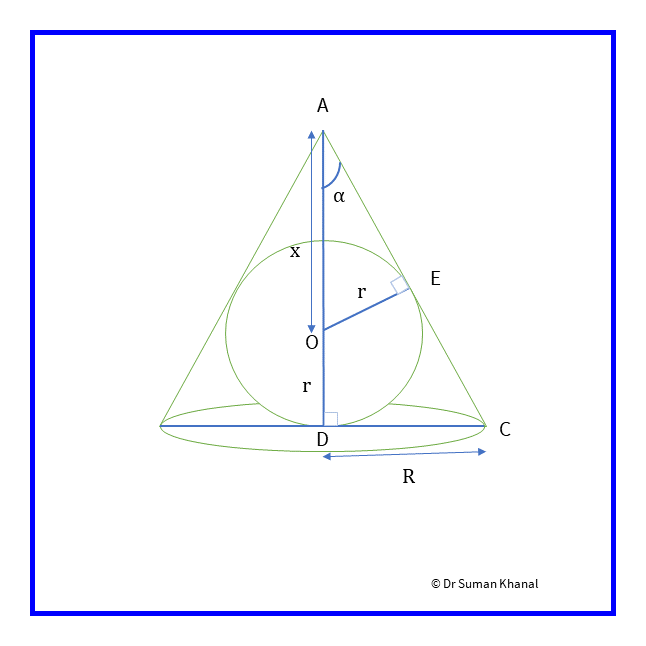
Figure 12.7: Cone circumscribed to a sphere of radius of $r$

From the figure we can make out $△AOE$ and $△ADC$ are similar. So,

$$\begin{array}{ccc}\frac{r}{R}& =\frac{AE}{AD}& =\frac{\sqrt{x^2-r^2}}{x+r}\\ R& =\frac{r(x+r)}{\sqrt{x^2-r^2}}& \end{array}$$

The volume of cone $V$ is given by,

$$\begin{array}{cc}V& =\frac{1}{3}\pi R^{2}h\\ & =\frac{1}{3}\pi \frac{r^2(x+r{)}^2}{x^2-r^2}(x+r)\\ & =\frac{1}{3}\pi \frac{r^2(x+r{)}^2(x+r)}{(x+r)(x-r)}\\ V& =\frac{1}{3}\pi \frac{r^2(x+r{)}^2}{x-r}\\ \frac{dV}{dx}& =\frac{1}{3}\pi r^2\frac{(x-r)2(x+r)-(x+r{)}^2}{(x-r{)}^2}\\ & =\frac{1}{3}\pi r^2\frac{(x+r)(2x-2r-x-r)}{(x-r{)}^2}\\ \frac{dV}{dx}& =\frac{1}{3}\pi r^2\frac{(x+r)(x-3r)}{(x-r{)}^2}& \text{(12.12)}\end{array}$$

For maximum or minimum value of $V$ w.r.t $x$,

$$\begin{array}{cc}\frac{dV}{dx}& =0\\ \frac{1}{3}\pi r^2\frac{(x+r)(x-3r)}{(x-r{)}^2}& =0\\ x& =-r,3r\end{array}$$

Dimension cannot be negative, so $x=3r$.

From equation (12.12), for a point in the immediate neighborhood of $x=3r$, $(x+r)$ and $(x-r{)}^2$ are positive. So the expression $(x-3r)$ determines the sign of $\frac{dV}{dx}$.

Value of $x$	$\frac{dV}{dx}$
$x<3r$	negative
$x>3r$	positive

So at point $x=3r$, $\frac{dV}{dx}$ changes sign from negative to positive, so the volume is minimum at this point.

From figure 12.7,

$$\begin{array}{cc}\sin \alpha & =\frac{\text{opposite}}{\text{hypotenuse}}\\ & =\frac{r}{x}\\ & =\frac{r}{3r}\\ \sin \alpha & =\frac{1}{3}\\ \alpha & ={\sin }^{-1}\left(\frac{1}{3}\right)\end{array}$$

12.1.9 Question 19

A cone is inscribed in a sphere of radius $r$, prove that its volume as well as well as its curve surface is greatest when its altitude is $\frac{4r}{3}$.

The given condition is depicted in figure 12.8.

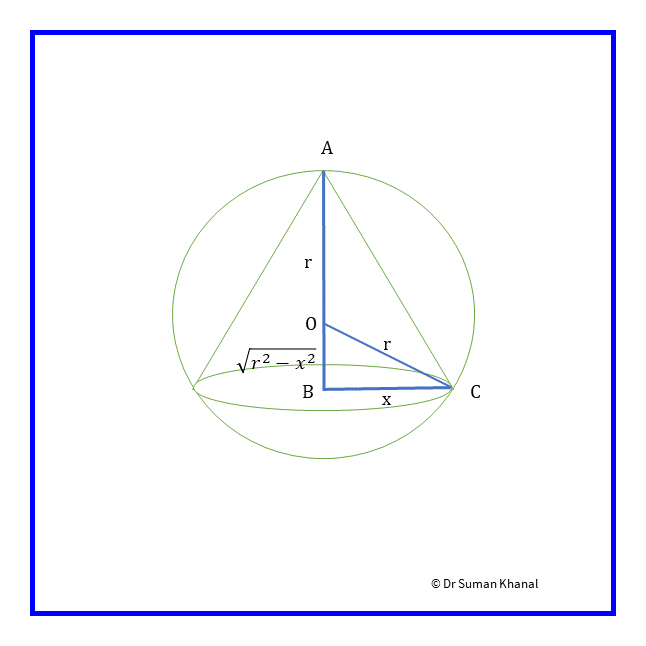
Figure 12.8: Cone inscribed in a sphere of radius $r$

From the figure, height $AB\left(h\right)$ of the cone is,

$$\begin{array}{cc}h& =\sqrt{r^2-x^2}+r\\ (h-r{)}^2& =(\sqrt{r^2-x^2}{)}^2\\ h^2-2hr+r^2& =r^2-x^2\\ x^2& =h(2r-h)\end{array}$$

First part

The volume of the cone is given by,

$$\begin{array}{cc}V& =\frac{1}{3}\pi x^{2}h\\ & =\frac{1}{3}\pi h(2r-h)\times h\\ V& =\frac{1}{3}\pi h^2(2r-h)\\ \frac{dV}{dh}& =\frac{1}{3}\pi [-h^2+(2r-h\left)2h\right]\\ \frac{dV}{dh}& =\frac{1}{3}\pi h(4r-3h)\end{array}$$

For extreme values of volume w.r.t height $h$ of cone,

$$\begin{array}{cc}\frac{dV}{dh}& =0\\ \frac{1}{3}\pi h(4r-3h)& =0\\ h& =\frac{4}{3}r\end{array}$$

At $h=\frac{4}{3}r$, $\frac{dV}{dh}$ changes sign from positive to negative. So volume is maximum at $h=\frac{4}{3}r$.

Second part

The curve surface of cone is,

$$\begin{array}{cc}S& =\pi xl\\ & =\pi x\sqrt{x^2+h^2}\\ & =\pi x\sqrt{2hr}\\ S^2& =(\pi x\sqrt{2hr}{)}^2\\ & ={\pi }^2{x}^2\times 2hr\\ S^2& ={\pi }^2(2hr-h^2)\times 2hr\\ S^2& =2{\pi }^2{h}^{2}r(2r-h)\\ 2S\frac{dS}{dh}& =2{\pi }^{2}r(-h^2+(2r-h\left)2h\right)\\ 2S\frac{dS}{dh}& =2{\pi }^{2}r(4hr-3h^2)\\ S\frac{dS}{dh}& ={\pi }^{2}rh(4r-3h)\end{array}$$

For extreme value of curve surface of cone,

$$\begin{array}{cc}\frac{dS}{dh}& =0\\ {\pi }^{2}rh(4r-3h)& =0\\ 3h& =4r\\ h& =\frac{4}{3}r\end{array}$$

At $h=\frac{4}{3}r$, $\frac{dS}{dh}$ changes sign from positive to negative. So curve surface of cone inscribed in a sphere is greatest when $h=\frac{4}{3}r$.

12.1.10 Question 20

For a given curve surface of a right cone, when the volume is maximum, prove that the semi-vertical angle is ${\sin }^{-1}\frac{1}{\sqrt{3}}$.

Figure 12.9: Right cone with slant height $l$ and radius $r$

From figure 12.9, for a given slant height $l$ of cone and radius $r$, the height of cone is given by,

$$\begin{array}{cc}h& =\sqrt{l^2-r^2}\end{array}$$

The volume of cone $V$ is given by,

$$\begin{array}{cc}V& =\frac{1}{3}\pi r^{2}h\\ & =\frac{1}{3}\pi r^2\left(\sqrt{l^2-r^2}\right)& \text{(12.13)}\end{array}$$

The curve surface of the cone $S$ which is given and constant is,

$$\begin{array}{}S& =\pi rl& \text{(12.14)}\end{array}$$

$$\begin{array}{cc}l& =\frac{S}{\pi r}\end{array}$$

Substituting this into equation (12.13),

$$\begin{array}{cc}V& =\frac{1}{3}\pi r^2\sqrt{\frac{S^2}{{\pi }^2{r}^2}-r^2}\\ & =\frac{1}{3}\pi r^2\frac{\sqrt{S^2-{\pi }^2{r}^4}}{\pi r}\\ V& =\frac{r}{3}\sqrt{S^2-{\pi }^2{r}^4}\\ V^2& =\frac{r^2}{9}(S^2-{\pi }^2{r}^4)\end{array}$$

Differentiating w.r.t $r$,

$$\begin{array}{cc}2V\frac{dV}{dr}& =\frac{1}{9}\left[2r\right(S^2-{\pi }^2{r}^4)+r^2(-4{\pi }^2{r}^3\left)\right]\\ 2V\frac{dV}{dr}& =\frac{1}{9}[2r{S}^2-2{\pi }^2{r}^5-4{\pi }^2{r}^5]\\ 2V\frac{dV}{dr}& =\frac{2}{9}[r{S}^2-3{\pi }^2{r}^5]\\ V\frac{dV}{dr}& =\frac{1}{9}[r{S}^2-3{\pi }^2{r}^5]\end{array}$$

Also,

$$\begin{array}{}V\frac{d^{2}V}{d{r}^2}+{\left(\frac{dV}{dr}\right)}^2& =\frac{1}{9}[S^2-15{\pi }^2{r}^4]& \text{(12.15)}\end{array}$$

For volume maxima or minima w.r.t $r$,

$$\begin{array}{cc}\frac{dV}{dr}& =0\\ \frac{1}{9}[r{S}^2-3{\pi }^2{r}^5]& =0\\ 3{\pi }^2{r}^4& =S^2\\ r& =\pm {\left(\frac{S^2}{3{\pi }^2}\right)}^{1/4}\end{array}$$

As radius cannot be negative, $r={\left(\frac{S^2}{3{\pi }^2}\right)}^{1/4}$.

For $r={\left(\frac{S^2}{3{\pi }^2}\right)}^{1/4}$, from equation (12.15),

$$\begin{array}{cc}\frac{d^{2}V}{d{r}^2}& =\text{negative}\end{array}$$

So, at $r={\left(\frac{S^2}{3{\pi }^2}\right)}^{1/4}$, volume of cone is maximum for a fixed curve surface area.

$$\begin{array}{cc}r& ={\left(\frac{S^2}{3{\pi }^2}\right)}^{1/4}\\ r^4& =\frac{S^2}{3{\pi }^2}\end{array}$$

Substituting values from equation (12.14),

$$\begin{array}{cc}{r}^4& =\frac{{\pi }^2{r}^2{l}^2}{3{\pi }^2}\\ r^2& =\frac{l^2}{3}\\ r& =\pm \frac{l}{\sqrt{3}}\end{array}$$

$r$ cannot be negative since it is a dimension, so $r=\frac{l}{\sqrt{3}}$.

From figure 12.9,

$$\begin{array}{cc}\sin \theta & =\frac{r}{l}\\ & =\frac{\frac{l}{\sqrt{3}}}{l}\\ \sin \theta & =\frac{1}{\sqrt{3}}\\ \theta & ={\sin }^{-1}\frac{1}{\sqrt{3}}\end{array}$$

Thus, for a given curve surface of a right cone, when the volume is maximum, the semi-vertical angle is ${\sin }^{-1}\frac{1}{\sqrt{3}}$.